6.7 KiB
Лабораторная работа 1. Вариант 4.
Задание
Построить графики, отобразить качество моделей, объяснить полученные результаты.
Данные: make_circles (noise=0.2, factor=0.5, random_state=rs)
Модели:
- Линейная регресся
- Полиномиальная регрессия (со степенью 4)
- Гребневая полиномиальная регресся (со степенью 4, alpha = 1.0)
Как запустить
Для запуска программы необходимо с помощью командной строки в корневой директории файлов прокета прописать:
python main.py
После будет запущена программа и сгенерированы 3 графика.
Используемые технологии
numpy(псевдонимnp): NumPy - это библиотека для научных вычислений в Python.matplotlib.pyplot(псевдонимplt): Matplotlib - это библиотека для создания статических, анимированных и интерактивных визуализаций в Python.pyplot- это модуль Matplotlib, который используется для создания графиков и диаграмм.matplotlib.colors.ListedColormap- этот модуль Matplotlib используется для создания цветных схем цветовых карт, которые могут быть использованы для визуализации данных.sklearn(scikit-learn): Scikit-learn - это библиотека для машинного обучения и анализа данных в Python. Из данной библиотеки были использованы следующие модули:model_selection- Этот модуль scikit-learn предоставляет инструменты для разделения данных на обучающие и тестовые наборы.linear_model- содержит реализации линейных моделей, таких как линейная регрессия, логистическая регрессия и другие.pipeline- позволяет объединить несколько этапов обработки данных и построения моделей в одну конвейерную цепочку.PolynomialFeatures- Этот класс scikit-learn используется для генерации полиномиальных признаков, позволяя моделям учитывать нелинейные зависимости в данных.make_circles- Эта функция scikit-learn создает набор данных, представляющий собой два класса, расположенных в форме двух пересекающихся окружностей. Это удобно для демонстрации работы различных моделей классификации.LinearRegression- линейная регрессия - это алгоритм машинного обучения, используемый для задач бинарной классификации.
Описание работы
Программа генерирует данные, разделяет данные на тестовые и обучающие для моделей по заданию.
rs = randrange(50)
X, y = make_circles(noise=0.2, factor=0.5, random_state=rs)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=rs)
X_train и y_train используются для обучения, а на данных X_test и y_test - оценка их качества.
Поскольку все модели в задании регрессионные, результаты работы будем оценивать через решение задачи предсказания.
Для оценки будем использовать следующие критерии: среднеквадратическому отклонению и коэфициенту детерминации. Чем ошибка меньше и чем коэфициент детерминации больше, тем лучше.
np.round(np.sqrt(metrics.mean_squared_error(y_test, y_predict)),3) #среднеквадратическое отклонение
np.round(metrics.r2_score(y_test, y_predict), 2) #коэфициент детерминации
Оценочные параметры округлены с помощью функции round до 3х и 2х знаков после запятой.
Линейная регрессия
Для создания модели линейной регрессии воспользуемся LinearRegression.
linear_reg = LinearRegression()
Обучим её и предскажем с её помощью y на тестовой выборке x_text.
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
График для оценки результатов:

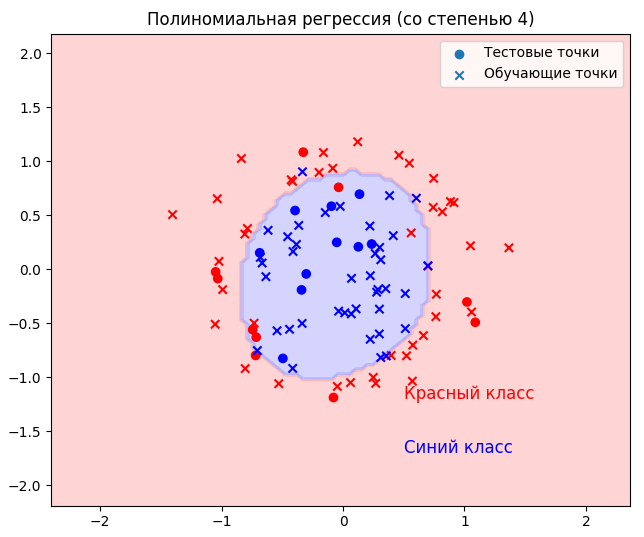
Полиномиальная регрессия
Добавим 3 недостающих члена к линейной модели, возведённых в соответствующие степени 2, 3 и 4.
poly_reg = make_pipeline(PolynomialFeatures(degree=4), StandardScaler(), LogisticRegression(random_state=rs))
График для оценки результатов:
Полиномиальная гребневая регрессия
Линейная регрессия является разновидностью полиномиальной регрессии со степенью ведущего члена равной 1.
ridge_poly_reg = make_pipeline(PolynomialFeatures(degree=4), StandardScaler(), LogisticRegression(penalty='l2', C=1.0, random_state=rs))
График для оценки результатов:

Вывод
Наиболее низкое среднеквадратичное отклонение и наиболее высокий коэффициент детерминации показала модель полиномиальной и полиномиальной гребневой регрессии. Это означает, что они являются лучшими моделями для данного набора данных.
