7.3 KiB
Лабораторная работа 1. Вариант 4.
Задание
Построить графики, отобразить качество моделей, объяснить полученные результаты.
Данные: make_moons (noise=0.3, random_state=rs)
Модели:
- Линейная регресся
- Полиномиальная регрессия (со степенью 4)
- Гребневая полиномиальная регресся (со степенью 4, alpha = 1.0)
Как запустить
Для запуска программы необходимо с помощью командной строки в корневой директории файлов прокета прописать:
python main.py
После этого в папке static сгенерируются 4 графика, по которым оценивается результат выполнения программы.
Используемые технологии
- Библиотека
pyplot, используемая для построения графиков. - Библиотека
sklearn- большой набор функционала для анализа данных. Из неё были использованы инструменты:make_moons- генератор случайных структурированных данныхtrain_test_split- разделитель данных на обучающиую и тестовую выборкиLinearRegression- инструмент работы с моделью "Линейная регрессия"Ridge- инструмент работы с моделью "Гребневая регрессия"PolynomialFeatures- инструмент работы с моделью "Полиномиальная регрессия"metrics- набор инструменов для оценки моделей
- Библиотека
numpy, используемая для обработки массивов данных и вычислений
Описание работы
Программа генерирует данные для обучения и тестирования моделей, стандартизирует данные и разделяет их на обучающую и тестовую выборки.
X, y = make_moons(noise=0.3, random_state=None)
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4, random_state=42)
После чего, на данных X_train и y_train производится обучение моделей, а на данных X_test и y_test - оценка их качества.
Поскольку все модели в задании регрессионные, результаты работы будем оценивать через решение задачи предсказания. Это позволит нам использовать для оценки только y данные, что облегчит построение графиков.
Оценка качества моделей будет производиться по двум критериям - среднеквадратическому отклонению mid_square от истинного результата и коэфициенту детерминации det_kp. Чем среднеквадратическая ошибка меньше и чем коэфициент детерминации больше, тем лучше модель показала себя на данной выборке.
mid_square = np.round(np.sqrt(metrics.mean_squared_error(y_test, y_predict)), 3)
det_kp = np.round(metrics.r2_score(y_test, y_predict), 2)
Где y_predict - решение задачи предсказания. Для наглядности, оценочные параметры округлим с помощью функции round до 3х и 2х знаков после запятой.
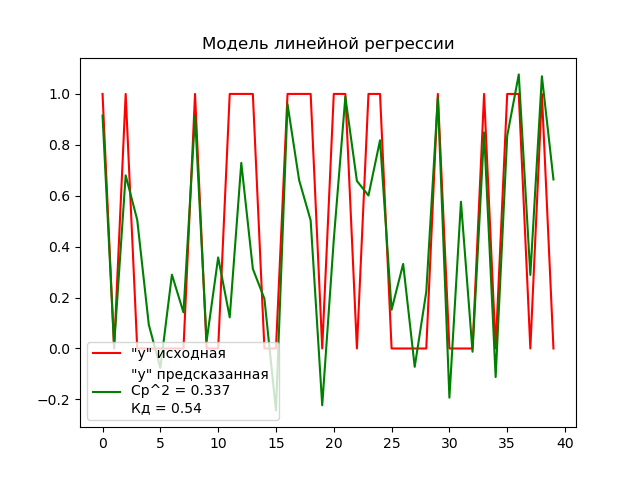
Линейная регрессия
Для создания модели линейной регрессии воспользуемся объектом LinearRegression(), обучим модель и заставим её предсказать значения y на тестовой выборке x_text.
linear = LinearRegression()
linear.fit(X_train, y_train)
y_predict = linear.predict(X_test)
Построим график для оценки результатов:
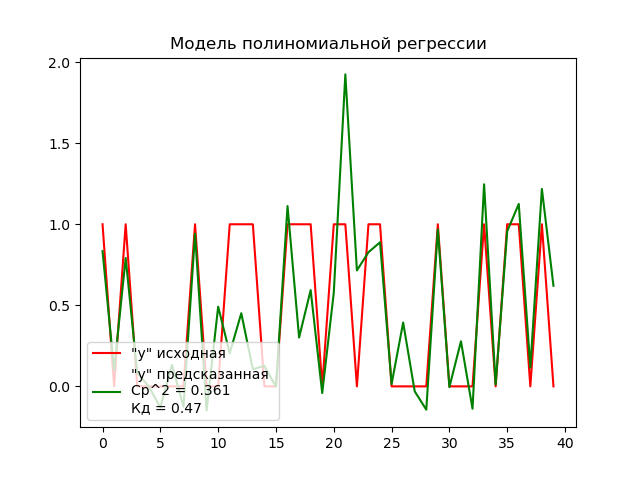
Полиномиальная регрессия
Линейная регрессия является разновидностью полиномиальной регрессии со степенью ведущего члена равной 1. Чтобы построить модель полиномиальной регрессии со степенью 4 необходимо к данным модели линейной регрессии добавить 3 недостающих члена, возведённых в соответствующие степени 2, 3 и 4.
poly = PolynomialFeatures(degree=4, include_bias=False)
x_poly_train = poly.fit_transform(X_train)
x_poly_test = poly.fit_transform(X_test)
Где degree - старшая степень полинома, include_bias - приведение свободного члена полинома к 0.
Обучение и прогнозирование модели далее производится также, как с моделью линейной регрессии, но уде на данных x_poly_train и x_poly_test
Построим график для оценки результатов:
Полиномиальная гребневая регрессия
Полиномиальная гребневая регрессия - это та же самая полиномиальная регрессия, но построенная с использованием усредняющего коэфициента. Для этого воспользуемся объёктом Ridge() и построим модель аналогично первым.
ridge = Ridge(alpha=1.0)
ridge.fit(x_poly_train, y_train)
y_predict = ridge.predict(x_poly_test)
Построим график для оценки результатов:
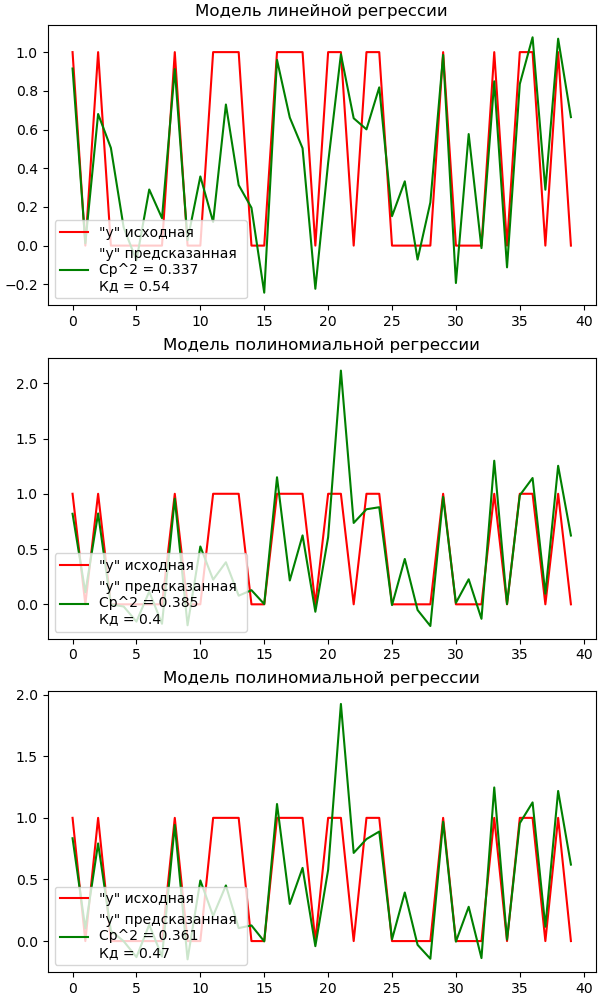
Теперь построим график для сравнения работы всех моделей и выберем наилучшую:
Вывод
Наиболее низкое среднеквадратичное отклонение и наиболее высокий коэфициент детерминации показала модель линейной регрессии, а это значит что она наилучшем образом подходит для работы со сгенерированным данными. В этом случае мы можем предположить что данные выборки находятся на небольшом расстоянии друг от друга и располагаются линейно.