8.2 KiB
Лабораторная работа №1. Вариант 4.
Задание
Сгенерируйте определенный тип данных и сравните на нем 3 модели (по варианту). Постройте графики, отобразите качество моделей, объясните полученные результаты.
Содержание
Введение
Это Flask-приложение создано для демонстрации работы различных моделей машинного обучения на сгенерированном наборе данных "Лунные данные". Приложение включает в себя веб-страницу, на которой можно посмотреть визуализацию результатов трех моделей (линейная регрессия, полиномиальная регрессия и гребневая полиномиальная регрессия).
Зависимости
Для работы этого приложения необходимы следующие библиотеки Python:
- Flask
- Matplotlib
- scikit-learn
- NumPy
- io
Вы можете установить их с помощью pip:
pip install flask matplotlib scikit-learn numpy
Запуск приложения
Чтобы запустить это Flask-приложение, выполните следующую команду:
python lab1-web.py
Приложение будет доступно по адресу http://localhost:5000 в вашем веб-браузере.
Описание кода
Создание данных
Для создания набора данных используется функция make_moons из scikit-learn. Данные представляют собой два класса, сгруппированных в форме лун, с добавлением шума. Затем данные нормализуются с использованием StandardScaler, и разделяются на обучающий и тестовый наборы данных.
Создание моделей
В коде определены три модели машинного обучения:
- Линейная регрессия.
- Полиномиальная регрессия четвертой степени. Она создается с использованием
PolynomialFeaturesи логистической регрессии. - Гребневая полиномиальная регрессия четвертой степени. Она также создается с использованием
PolynomialFeatures, но с добавлением регуляризации (гребня) в логистической регрессии.
Обучение и оценка моделей
Модели обучаются на обучающем наборе данных, и их точность оценивается на тестовом наборе данных с использованием метрики accuracy_score, показывающей точность моделей. Результаты оценки сохраняются в словаре model_results, который содержит информацию о точности модели и тестовых данных.
Веб-приложение
Приложение реализовано с использованием Flask:
- маршрут:
/- главная страница, на которой отображаются результаты работы моделей.
Использование
-
Запустите приложение, как описано выше.
-
Перейдите по адресу
http://localhost:5000в вашем веб-браузере. -
На главной странице вы увидите результаты работы всех трех моделей, включая их точность.
Модели
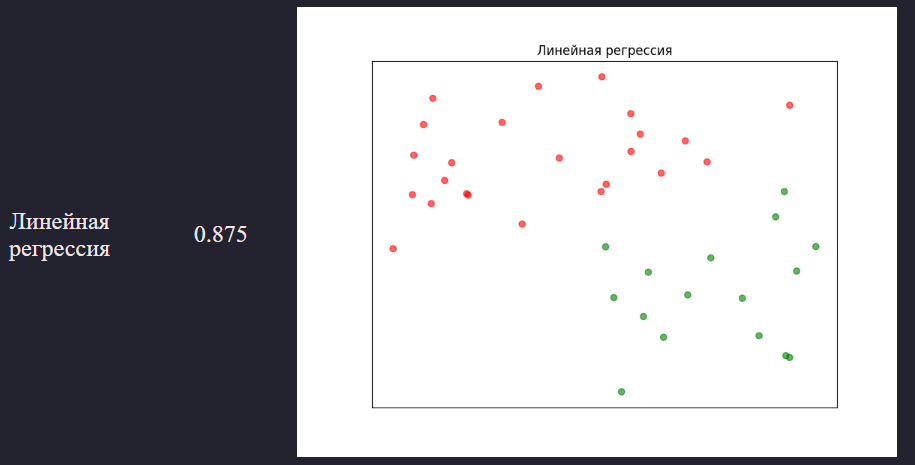
Линейная регрессия
Модель создается следующим образом:
"Линейная регрессия": LogisticRegression()
Результат в виде графика:
Точность полученной модели получилась равной 0.875
Полиномиальная регрессия
Код создания модели:
"Полиномиальная регрессия": make_pipeline(PolynomialFeatures(degree=4), LogisticRegression())
Результат в виде графика:
Точность полученной модели получилась равной 0.85
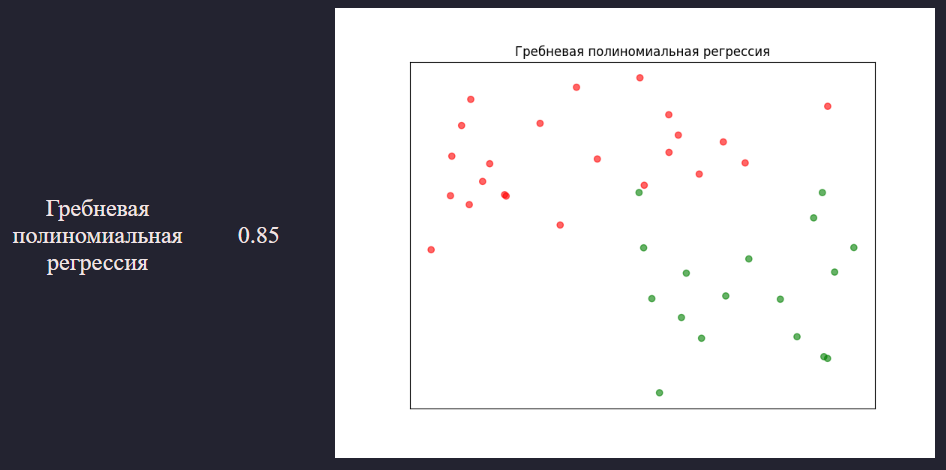
Гребневая полиномиальная регрессия
Код создания модели:
"Гребневая полиномиальная регрессия": make_pipeline(PolynomialFeatures(degree=4), LogisticRegression(penalty='l2', C=1.0))
Результат в виде графика:
Точность полученной модели получилась равной 0.85
Заключение
Все полученные модели:
- "Линейная регрессия" продемонстрировала самую высокую точность среди всех трех моделей (0.875).
- Это означает, что линейная модель достаточно хорошо справляется с задачей классификации данных.
- Это может быть следствием хорошо структурированных данных.
- "Полиномиальная регрессия" и "Гребневая полиномиальная регрессия" имеют одинаковую точность (0.85).
- Обе эти модели показали одинаково хорошие результаты и считаются весьма точными для данной задачи.
- Это может свидетельствовать о наличии нелинейных зависимостей в данных, которые успешно извлечены благодаря использованию полиномиальных признаков и гребневой регуляризации.
- В данном контексте различие между "Полиномиальной регрессией" и "Гребневой полиномиальной регрессией" может быть незначительным, так как точность одинакова.
- Модели смогли достичь высокой точности, что может указывать на наличие явных зависимостей между признаками и целевой переменной.