| .. | ||
| main.py | ||
| README.md | ||
| report.png | ||
Лабораторная работа №6
Задание
Реализовать последователный и параллельный алгоритм поиска детерминанта матрицы размером 100x100, 300x300, 500x500 элементов, сравнить результаты.
Описание алгоритмов
Последовательное поиск детерминанта
- Использует метод Гаусса для приведения матрицы к верхней треугольной форме. Детерминант равен произведению элементов на диагонали. Время работы — O(n³).
Параллельное поиск детерминанта
- Разделяет матрицу на блоки, каждый из которых обрабатывается отдельным потоком.
Поиск с использованием библиотеки Numpy
- Использует оптимизированную функцию np.linalg.det, которая применяет методы, такие как LU-разложение, для быстрого вычисления детерминанта.
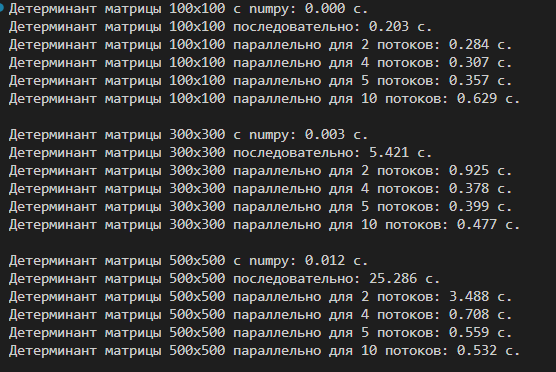
Результаты
Вывод
- Параллельное умножение матриц эффективно при работе с большими матрицами при увеличении потоков.
- Последовательное умножение матриц эффективно использовать при меньших размерах матриц, где выйгрыш от управления потоками минимален.
- Numpy показал блестящий результат.