Отчет по лабораторной работе №6

Описание задачи

Данная работа нацелена на изучение эффективности параллельных вычислений при нахождении детерминанта квадратной матрицы. Были реализованы два алгоритма:

Последовательный алгоритм: рекурсивное вычисление детерминанта методом разложения по строкам.
Параллельный алгоритм: вычисление детерминанта с использованием многопоточности, где различные миноры матрицы вычисляются в отдельных потоках.

Целью эксперимента было сравнение времени выполнения последовательного и параллельного алгоритмов для матриц разного размера и с разным количеством потоков.

Структура проекта

Проект состоит из двух файлов с реализацией алгоритмов:

regular.go (в папке alg) — рекурсивное вычисление детерминанта методом разложения по строкам.
parallel.go (в папке alg) — вычисление детерминанта с использованием многопоточности, где различные миноры матрицы вычисляются в отдельных потоках.
matrix.go (в папке util) — вспомогательные функции для матриц.
run.go - запуск бенчмарков.

Результаты

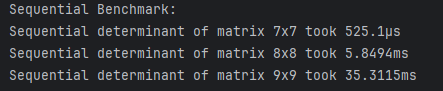
Последовательный алгоритм

Размер матрицы	Время выполнения
7x7	525.1µs
8x8	5.8494ms
9x9	35.3115ms

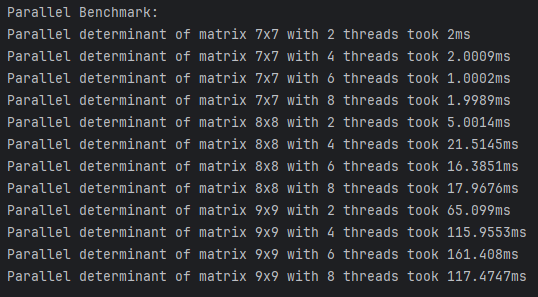
Параллельный алгоритм

Размер матрицы	Количество потоков	Время выполнения
7x7	2	2ms
7x7	4	2.0009ms
7x7	6	1.0002ms
7x7	8	1.9989ms
8x8	2	5.0014ms
8x8	4	21.5145ms
8x8	6	16.3851ms
8x8	8	17.9676ms
9x9	2	65.099ms
9x9	4	115.9553ms
9x9	6	161.408ms
9x9	8	117.4747ms

Анализ полученных данных

Последовательный алгоритм:

Последовательный алгоритм показал ожидаемую тенденцию: с увеличением размера матрицы, время выполнения увеличивается экспоненциально. Это связано с тем, что сложность рекурсивного алгоритма вычисления детерминанта составляет O(n!), где n — размер матрицы. Даже небольшое увеличение размера матрицы приводит к значительному росту времени вычислений.
Параллельный алгоритм:

Матрицы 7x7:
- Время параллельного алгоритма оказалось больше, чем последовательного. Это связано с тем, что накладные расходы на создание потоков, синхронизацию данных и распределение задач превышают выгоду от параллельного выполнения для небольших задач. Матрица 7x7 слишком мала, чтобы эффективно распределить вычисления между потоками, поэтому многопоточность не дает прироста в производительности.
Матрицы 8x8:
- Параллельное вычисление снова оказалось медленнее последовательного. Время выполнения с увеличением количества потоков увеличивалось вплоть до 4 потоков, что демонстрирует отрицательный эффект от создания избыточного числа потоков для задач такого размера. Наибольшее ускорение удалось достичь с 2 и 6 потоками, но даже в этом случае результат (5.0014 и 16.3851 ms) был хуже и менее стабильным последовательного (5.8494 ms).
Матрицы 9x9:
- Здесь также наблюдается значительное замедление при увеличении количества потоков. Время с 8 потоками составило 117.4747 ms, что все равно больше времени последовательного алгоритма (35.3115 ms). Это связано с тем, что при увеличении числа потоков на задаче, где каждая операция по вычислению минора требует больших вычислительных затрат, накладные расходы на управление потоками могут стать слишком велики.

Демонстрационное видео

Видеозапись доступна по адресу: https://vk.com/video193898050_456240874

6.4 KiB Raw Blame History Unescape Escape