3.4 KiB
Лабораторная работа 6 - Параллельный поиск значения детерминанта матрицы
ПИбд-42 || Алейкин Артем
Описание
В данной лабораторной работе мы занимались написанием многопоточного вычислителя детерминанта больших матриц.
Объяснения
Последовательный алгоритм: Нахождение детерминанта реализовано рекурсивно через формулу разложения по строке матрицы. Метод DeterminantSequential вычисляет детерминант через разложение по первой строке и вызов минора.
static double DeterminantSequential(double[,] matrix)
{
int size = matrix.GetLength(0);
if (size == 1)
return matrix[0, 0];
if (size == 2)
return matrix[0, 0] * matrix[1, 1] - matrix[0, 1] * matrix[1, 0];
double determinant = 0;
for (int col = 0; col < size; col++)
{
determinant += Math.Pow(-1, col) * matrix[0, col] * DeterminantSequential(Minor(matrix, 0, col));
}
return determinant;
}
Параллельный алгоритм: Каждую итерацию разложения по строке матрицы можно выполнять в отдельном потоке. DeterminantParallel использует Parallel.For для запуска потоков.
static double DeterminantParallel(double[,] matrix, int threadCount)
{
int size = matrix.GetLength(0);
if (size == 1)
return matrix[0, 0];
if (size == 2)
return matrix[0, 0] * matrix[1, 1] - matrix[0, 1] * matrix[1, 0];
double determinant = 0;
object lockObject = new object();
Parallel.For(0, size, new ParallelOptions { MaxDegreeOfParallelism = threadCount }, col =>
{
double minorDeterminant = DeterminantSequential(Minor(matrix, 0, col));
double term = Math.Pow(-1, col) * matrix[0, col] * minorDeterminant;
lock (lockObject)
{
determinant += term;
}
});
return determinant;
}
Миноры: Метод Minor создает подматрицу, исключая заданные строку и столбец.
static double[,] Minor(double[,] matrix, int row, int col)
{
int size = matrix.GetLength(0);
var minor = new double[size - 1, size - 1];
for (int i = 0, minorRow = 0; i < size; i++)
{
if (i == row) continue;
for (int j = 0, minorCol = 0; j < size; j++)
{
if (j == col) continue;
minor[minorRow, minorCol] = matrix[i, j];
minorCol++;
}
minorRow++;
}
return minor;
}
В результате мы получаем следующие значения:
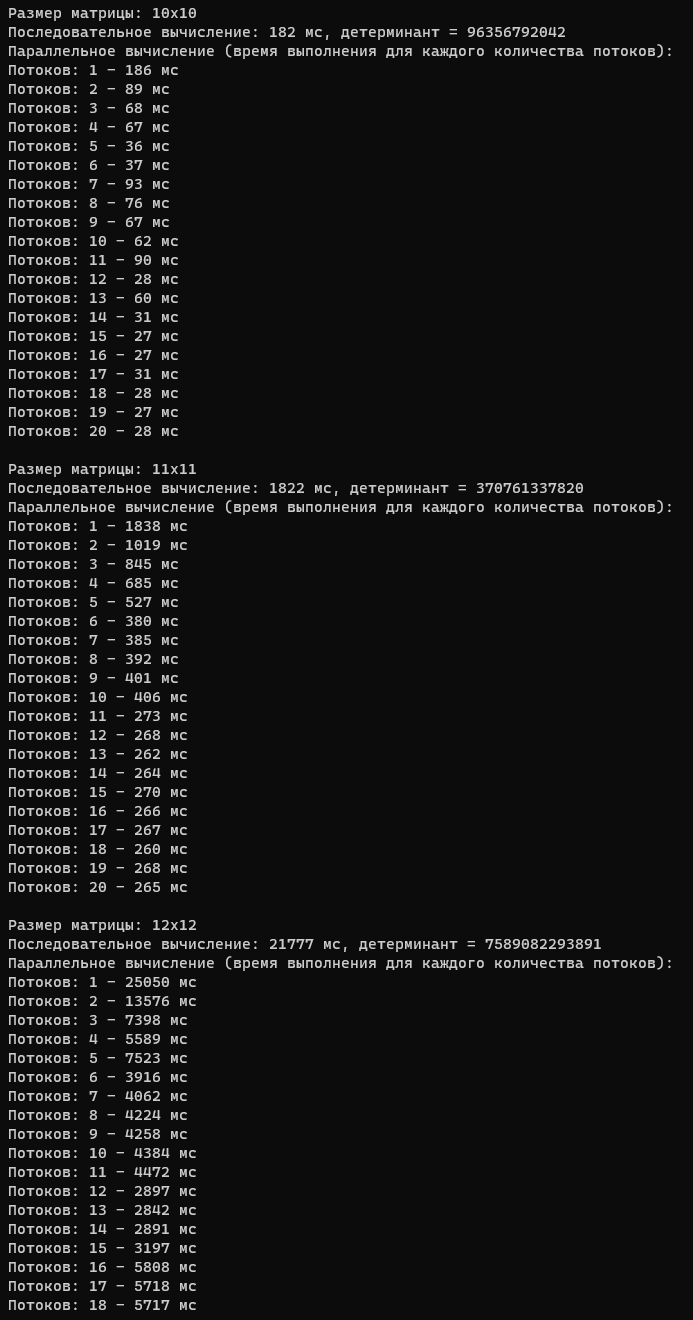
Результаты аналогичны с предыдущей лабораторной работой, многопоточный подход позволяет кратно выигрывать время, но и ресурсы на организацию работы всех потоков тоже существенны.
Видео демонстрации работы: https://vk.com/video248424990_456239613?list=ln-tyTv9vKdAOzQyPm5Y3