Alexey/DAS_2023_1
2
1
Fork 1
Code Issues Pull Requests 52 Packages Projects Releases Wiki Activity
a5f9016bb5
DAS_2023_1/antonov_dmitry_lab_6/README.md
DmitriyAntonov 4f5586f9ac antonov_dmitry_lab_6_ready
2023-12-05 13:37:52 +04:00

4.0 KiB
Raw Blame History

Лабораторная работа №6 - Определение детерминанта матрицы с помощью параллельных вычислений

Изучение параллельного вычисления дискриминанта

Задачи

Кратко: реализовать нахождение детерминанта квадратной матрицы.

Подробно: в лабораторной работе требуется сделать два алгоритма: обычный и параллельный (задание со * - реализовать это в рамках одного алгоритма). В параллельном алгоритме предусмотреть ручное задание количества потоков (число потоков = 1 как раз и реализует задание со *), каждый из которых будет выполнять нахождение отдельной группы множителей.

Сделать несколько бенчмарков последовательного и параллельного алгоритма поиска детерминанта матрицы размером 100x100, 300x300, 500x500 элементов.

Запуск

Проект запускается в ide просто по нажатию у питон файла на функцию мейн. Нужно последовательно запустить функцию мейн у файлов parallel_determ.py.

Описание работы:

Приложение представляет собой консольное приложение для вычисления детерминанта рандомной матрицы с числами определенного диапазона и размера матрицы. В программе предусмотрена возможность задания количества процессов для распараллеливания. Используется библиотека python multiprocessing.

На рис 3 видно, что с использованием параллельного алгоритма скорость обработки увеличивается довольно существенно. Но оптимальная скорость достигается при кол-ве потоков = кол-ву потоков процессора У меня их 8.

Вводим значения в скрипт

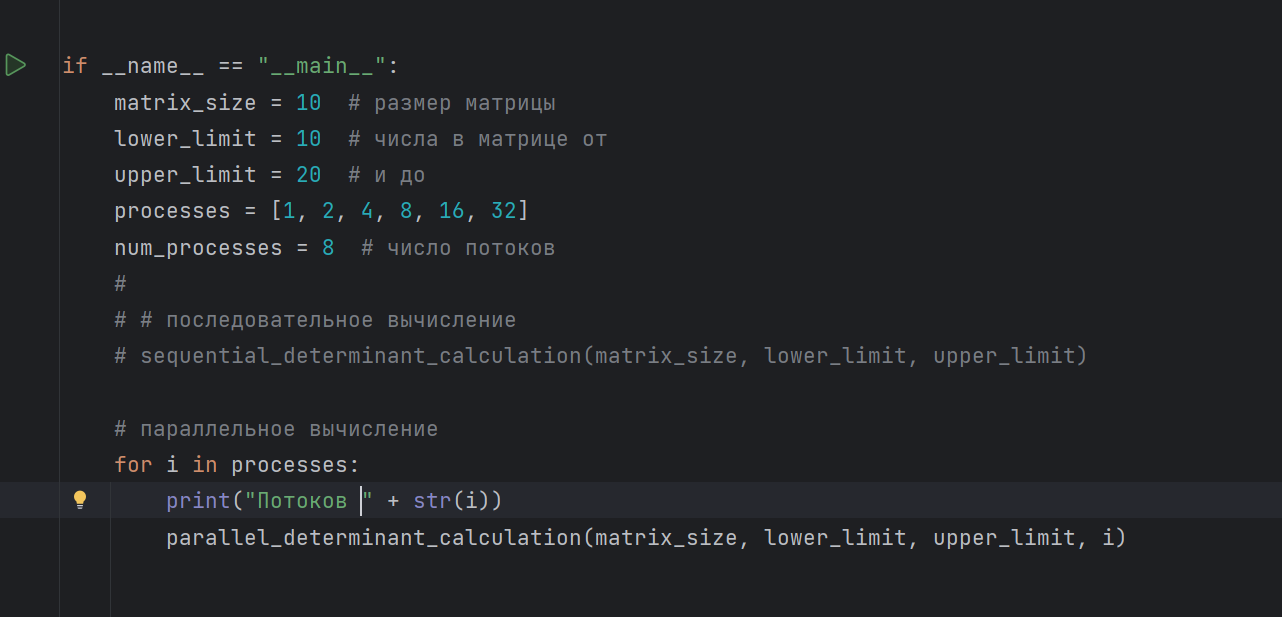
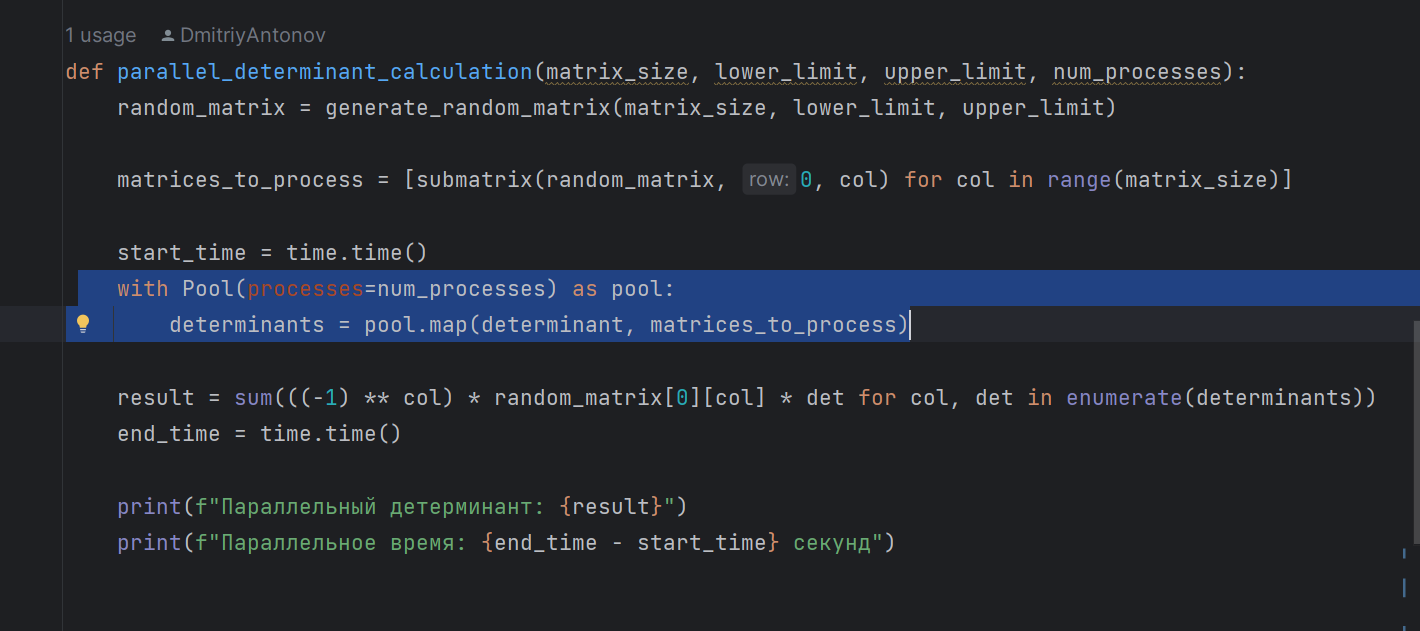
Параллельное умножение в коде

Сравнение бенчмарков

  • Размер матрицы для эксперимента 10*10
  • Потоков 1
  • Параллельный детерминант: 195955762.2581097
  • Параллельное время: 5.735873222351074 секунд
  • Потоков 2
  • Параллельный детерминант: 4409801072.873513
  • Параллельное время: 3.585620164871216 секунд
  • Потоков 4
  • Параллельный детерминант: -219763547.41593504
  • Параллельное время: 2.174274206161499 секунд
  • Потоков 8
  • Параллельный детерминант: 2067674869.5092595
  • Параллельное время: 1.8252685070037842 секунд
  • Потоков 16
  • Параллельный детерминант: 653887070.4597099
  • Параллельное время: 1.887946605682373 секунд
  • Потоков 32
  • Параллельный детерминант: 802268193.971918
  • Параллельное время: 3.3444454669952393 секунд

Ссылка на видео

https://disk.yandex.ru/i/PMBcmHiqJEjAcg