7.4 KiB
Лабораторная работа 5.
Задание
Задачи:
Реализовать умножение двух больших квадратных матриц. Сделать два алгоритма: обычный и параллельный (задание со * - реализовать это в рамках одного алгоритма). В параллельном алгоритме предусмотреть ручное задание количества потоков (число потоков = 1 как раз и реализует задание со *), каждый из которых будет выполнять умножение элементов матрицы в рамках своей зоны ответственности.
Как запустить лабораторную работу
В директории с файлом характеристик docker-compose.yaml выполнить команду:
docker-compose -f docker-compose.yaml up
Описание лабораторной работы
Для реализации параллельного умножения матриц с использованием многопоточности создадим несколько функций:
- Функция
multiplication_rows(row, matrix_b)
Данная функция используется для перемножения входной строки row на матрицу matrix_b и возвращает результат умножения.
def multiplication_rows(row, matrix_b):
return np.dot(row, matrix_b)
- Функция
parallel_matrix_multiplication(matrix_a, matrix_b, num_threads)
Данная функция Принимает две матрицы matrix_a и matrix_b, а также количество потоков num_threads, которое ровно количеству строк в первой матрице. Также осуществляется проверка на то, что размеры матрицы совместимы.
Затем создается пул потоков с использованием concurrent.futures.ThreadPoolExecutor и устанавливает максимальное количество потоков равным num_threads. Запускается таймер для измерения времени выполнения умножения матриц. Создается список results и
для каждой строки матрицы matrix_a запускает функцию multiplication_rows в отдельном потоке с помощью executor.submit(). Результаты сортируются по индексу строки и объединяются в матрицу в правильном порядке с помощью np.vstack(). Завершается таймер и происходит замер времени, затраченного на выполнение задачи.
def parallel_matrix_multiplication(matrix_a, matrix_b, num_threads):
num_rows_a, num_cols_a = matrix_a.shape
num_rows_b, num_cols_b = matrix_b.shape
assert num_cols_a == num_rows_b, "Размеры матриц несовместимы"
with concurrent.futures.ThreadPoolExecutor(max_workers=num_threads) as executor:
start_time = time.time()
results = []
for i in range(num_rows_a):
result = executor.submit(multiplication_rows, matrix_a[i], matrix_b)
results.append((i, result))
sorted_results = sorted(results, key=lambda x: x[0])
result_matrix = np.vstack(
[result.result() for _, result in sorted_results])
end_time = time.time()
execution_time = end_time - start_time
return result_matrix, execution_time
- Функция
test(parallel)
Данная функция создает две матрицы с фиксированными значениями. И происходит разбиение на два алгоритма вычисления умножения матриц: обычный и параллельный.Если parallel равно True, вызывает parallel_matrix_multiplication() с num_threads=2, иначе с num_threads=1.
- Функции
matrix100x100(parallel),matrix300x300(parallel)иmatrix500x500(parallel)
В данных функция создается пара случайных матриц размером 100x100, 300x300 и 500x500 со значениями от 0 до 100.
Если parallel равно True, вызывают parallel_matrix_multiplication() с num_threads равным размеру матрицы, иначе с num_threads=1.
Выводят результат умножения и время выполнения.
Пример функции для матрицы размером 100x100:
def matrix100x100(parallel):
a = np.random.randint(0, 100, size=(100, 100))
b = np.random.randint(0, 100, size=(100, 100))
if parallel:
result = parallel_matrix_multiplication(a, b, num_threads=100)
else:
result = parallel_matrix_multiplication(a, b, num_threads=1)
print("Результат умножения:")
print(result[0])
print("Время выполнения: " + str(result[1]) + " с")
Результаты выполнения последовательного и параллельного алгоритма на умножение двух матриц размером 100x100, 300x300, 500x500 элементов.
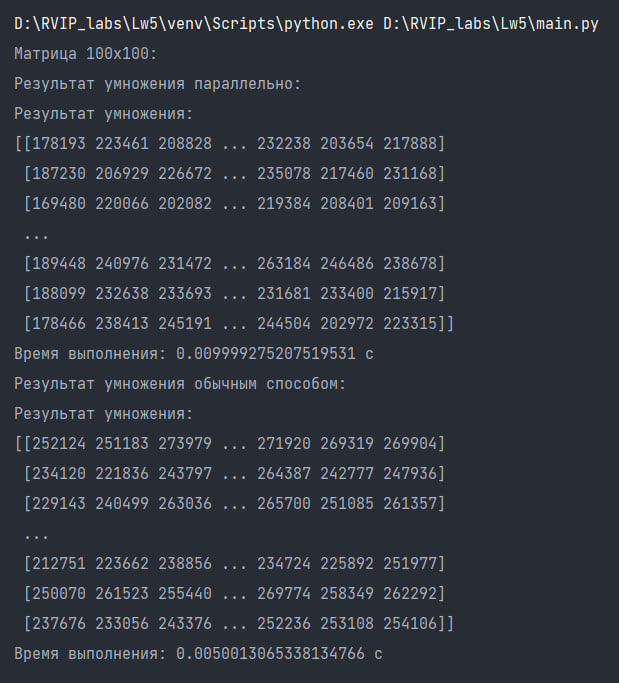
Результат перемножения матриц 100х100:
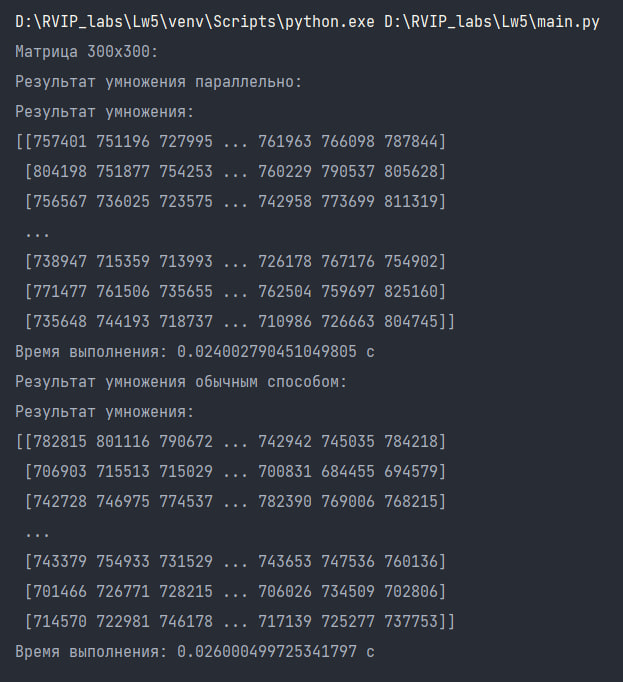
Результат перемножения матриц 300х300:
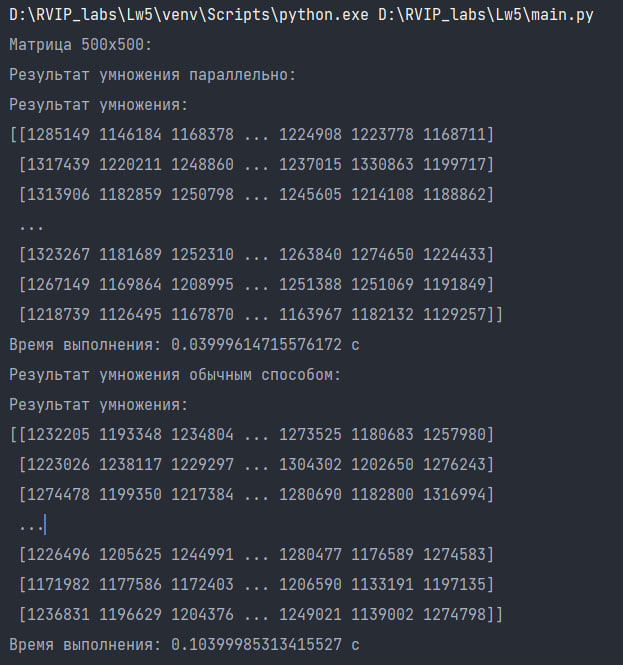
езультат перемножения матриц 500х500:
Таким образом, можно сделать вывод о том, что умножение матрицы параллельным способом значительно ускоряет процесс выполнения по сравнению с обычным способом на больших объемах данных. В случае матрицы размером 500х500, время выполнения параллельного умножения составляет всего 0.03999614715576172 с, в то время как обычный способ занимает 0.10399985313415527 с. Однако случае матрицы размером 100х100, время выполнения параллельного умножения составляет 0.008999347686767578 с, в то время как обычный способ занимает 0.006066799163818359 с, и перемножение обычным алгоритмом является более выгодным по временнным затратам, чем паралелльным. Параллельное умножение матрицы может быть полезным в случаях, когда требуется обработать большие объемы данных и ускорить процесс вычислений.