DAS_2023_1/tepechin_kirill_lab_6/README.md

Лабораторная работа №6, Тепечин Кирилл

Код

Обычный код

private static BigDecimal findDeterminantGauss(double[][] matrix) {
        int n = matrix.length;
        BigDecimal det = BigDecimal.ONE;

        for (int i = 0; i < n; i++) {
            int maxRow = i;
            for (int j = i + 1; j < n; j++) {
                if (Math.abs(matrix[j][i]) > Math.abs(matrix[maxRow][i])) {
                    maxRow = j;
                }
            }

            if (maxRow != i) {
                double[] temp = matrix[i];
                matrix[i] = matrix[maxRow];
                matrix[maxRow] = temp;

                det = det.multiply(BigDecimal.valueOf(-1));
            }

            for (int j = i + 1; j < n; j++) {
                double factor = matrix[j][i] / matrix[i][i];
                for (int k = i; k < n; k++) {
                    matrix[j][k] -= factor * matrix[i][k];
                }
            }
        }

        for (int i = 0; i < n; i++) {
            det = det.multiply(BigDecimal.valueOf(matrix[i][i]));
        }

        return det;

    }

Параллельный код

private static BigDecimal findDeterminantGaussParallel(double[][] matrix, int threadsCount) {
        int n = matrix.length;
        final BigDecimal[] det = {BigDecimal.ONE};

        ExecutorService executor = Executors.newFixedThreadPool(threadsCount);

        for (int i = 0; i < n; i++) {
            final int rowIdx = i;

            int maxRow = rowIdx;
            for (int j = rowIdx + 1; j < n; j++) {
                if (Math.abs(matrix[j][rowIdx]) > Math.abs(matrix[maxRow][rowIdx])) {
                    maxRow = j;
                }
            }

            if (maxRow != rowIdx) {
                double[] temp = matrix[rowIdx];
                matrix[rowIdx] = matrix[maxRow];
                matrix[maxRow] = temp;
                det[0] = det[0].multiply(BigDecimal.valueOf(-1));
            }
            executor.execute(() -> {
                for (int j = rowIdx + 1; j < n; j++) {
                    double factor = matrix[j][rowIdx] / matrix[rowIdx][rowIdx];
                    for (int k = rowIdx; k < n; k++) {
                        matrix[j][k] -= factor * matrix[rowIdx][k];
                    }
                }
            });
            det[0] = det[0].multiply(BigDecimal.valueOf(matrix[rowIdx][rowIdx]));
        }

        executor.shutdown();

        try {
            executor.awaitTermination(1, TimeUnit.DAYS);
        } catch (InterruptedException e) {
            e.printStackTrace();
        }

        return det[0];

    }

Тесты

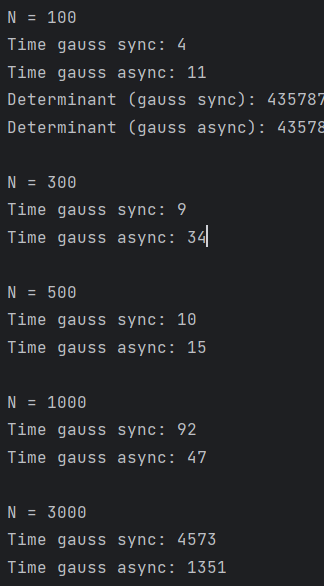
Тесты проводились на 16 потоках

Выводы

• На матрицах от 100 до 500 последовательное вычисление быстрее.

• Параллельное вычисление работает быстрее на матрицах от 1000 n.

Ссылка на видео

https://youtu.be/ZK1qSvbUNTk