compute-math/lab2

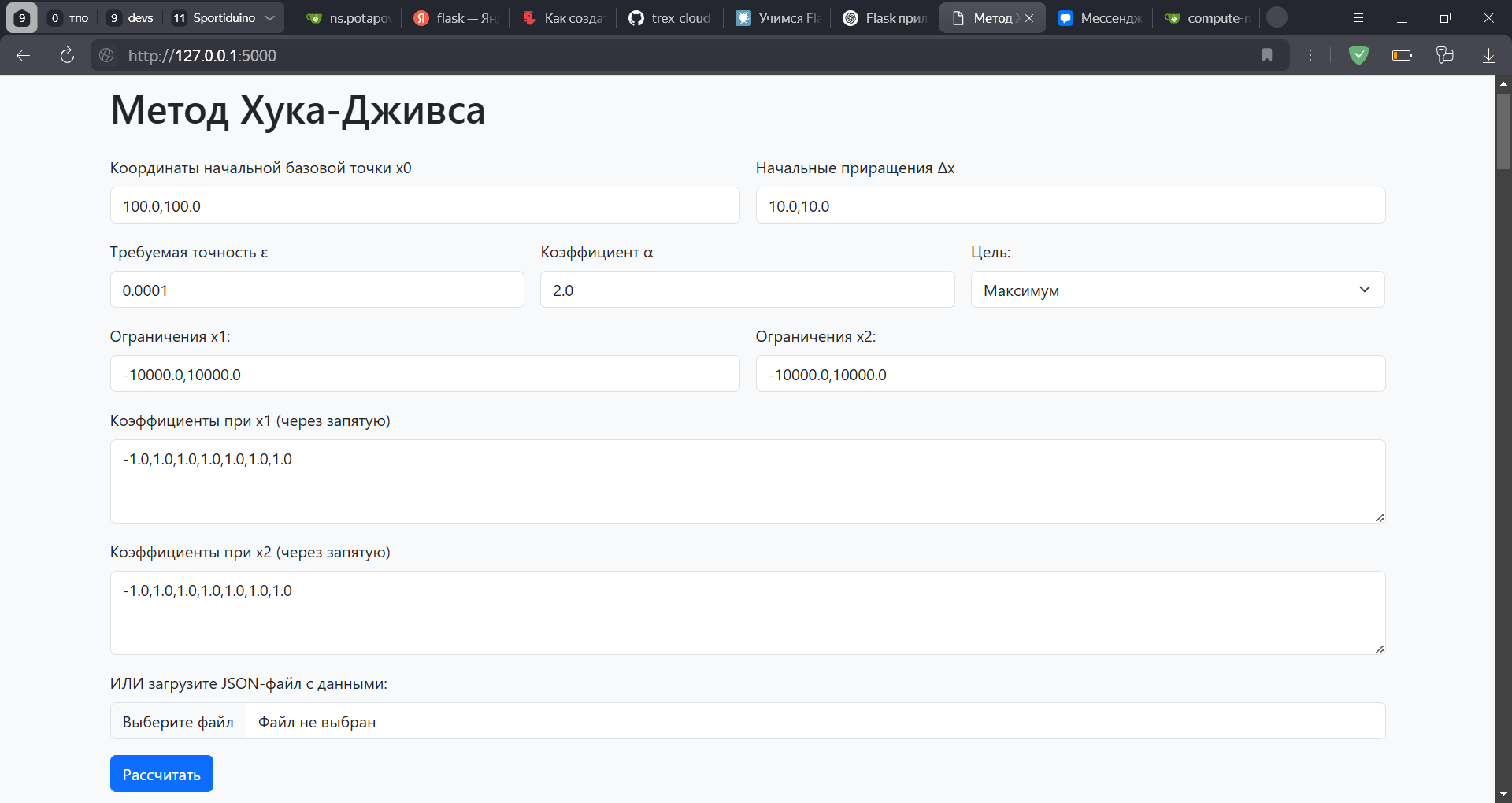
Лабораторная работа по вычислительной математике "Нелинейное программирование"

Запуск

Склонировать проект и перейти в директорию проекта

Для запуска проекта используется менеджер пакетов poetry

git clone ... project
cd project
poetry install
poetry run flask run

После запуска перейти по ссылке http://127.0.0.1:5000

Пример файла example.json с исходными данными

{
    "x0": [
        100,
        100
    ],
    "delta0": [
        10,
        10
    ],
    "epsilon": 0.0001,
    "alpha": 2,
    "target": "min",
    "x1r": [
        -10000,
        10000
    ],
    "x2r": [
        -10000,
        10000
    ],
    "x1c": [
        1,
        1,
        1,
        1,
        1,
        1,
        1
    ],
    "x2c": [
        1,
        1,
        1,
        1,
        1,
        1,
        1
    ]
}

Организация работы

1. Лабораторная работа выполняется индивидуально.
2. Лабораторная работа состоит из двух частей, основная часть и дополнительные задания в зависимости от качества выполнения работы.
3. Выбрать можно любой из предложенных вариантов, которые отличаются уровнем сложности и, как следствием, максимальным числом баллов, которое можно получить за выполнение.
4. Оценивается результат выполнения, а не качество написанного кода. Допускается реализация на любом языке программирования или среде разработки позволяющей решить задачу (1С, Excel, MatLAB, Maple и тд). Например, можно использовать макросы в Excel, но нельзя использовать готовый плагин для решения задач.
5. Допускается использование математических библиотек и пакетов реализующих вспомогательные функции, такие как операции с векторами и матрицами, вычисление градиента и Гессиана, основные математические функции. Использование готовых методов оптимизации не допускается.

Общее задание

1. Необходимо составить программную реализацию одного из изученных методов оптимизации полиномиальной функции с оценкой абсолютной погрешности работы данного метода.
2. Программа должна позволять ввести произвольные значения в заранее подготовленный файл, с клавиатуры или другим общепринятым способом. Генерация случайных данных не допускается.
3. Количество ненулевых коэффициентов в проверочных примерах должно быть не менее 10.
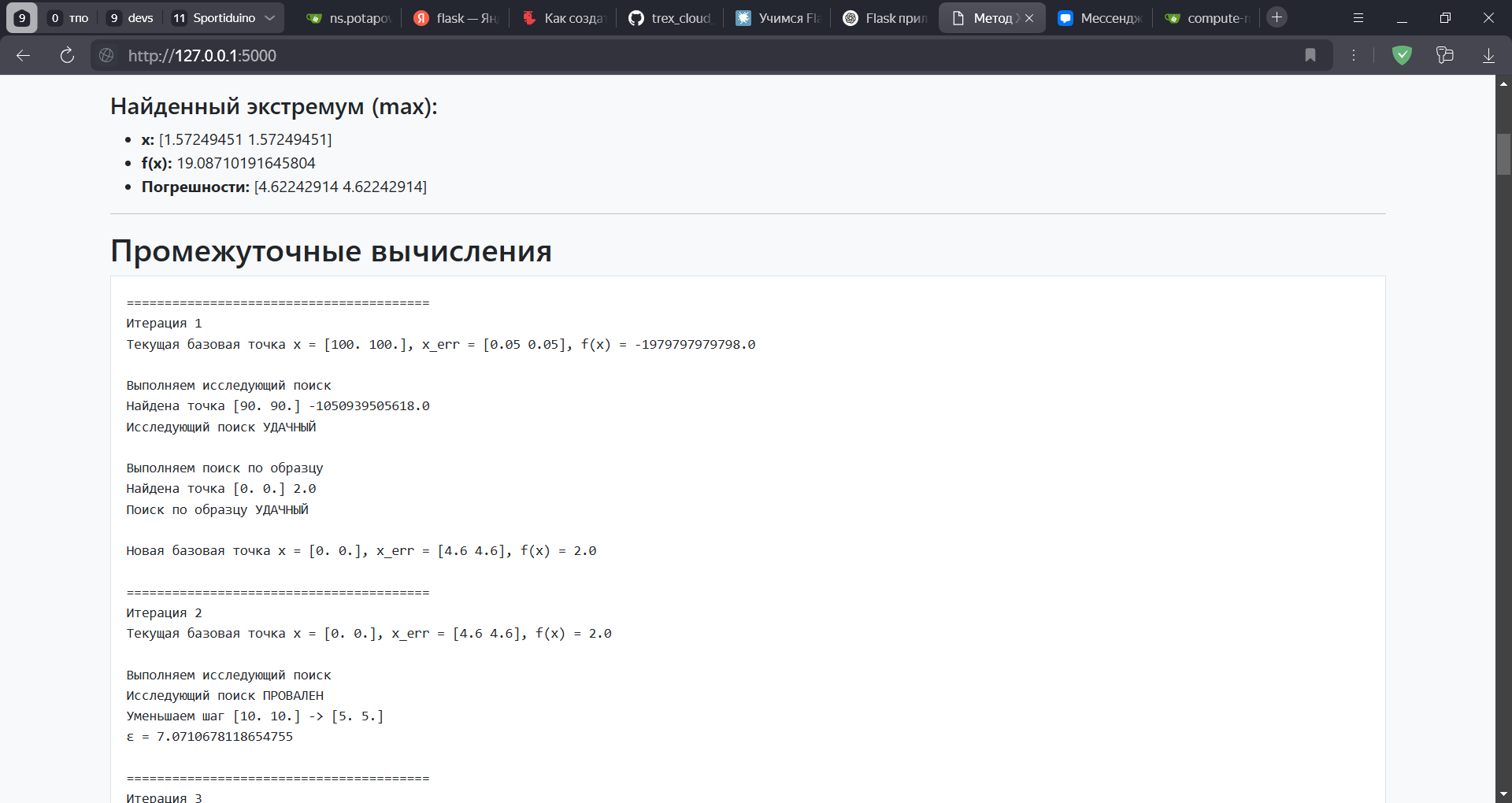
4. Результатом работы программы должны быть:
   • Значения неизвестных (массив X) для минимума и максимума функции на заданном отрезке.
   • Результаты подстановки неизвестных целевую функцию
   • Оценки абсолютных погрешностей для найденных значений
   • Поощряется вывод промежуточных вычислений и графиков функции.
5. Полученные абсолютные погрешности вычислений должны быть допустимыми, то есть не превышать половины единицы измерения искомых величин (не превышать 5%).

Пояснения по расчету погрешностей

1. Для расчета погрешностей необходимо использовать формулы из соответствующей лекции со слайдов 7 и 8. Так как все алгоритмы подразумевают только выполнения базовых математических операций, то формулы со слайда 9, вам скорее всего не пригодятся.
2. Погрешности исходных данных считаются по умолчанию и равны половине последнего введенного знака. То есть для числа 48 абсолютная погрешность равна 0.5, а для числа 48.01 абсолютная погрешность равна 0.005. Отдельно вводить погрешности для входных данных не требуется. Таким образом для достижения требуемого результата значения на входе должны иметь достаточно малые абсолютные погрешности.
3. Для косвенной само-проверки расчета погрешностей разумно подсчитывать общее количество операций сложения, вычитания, умножения и деления. Это позволит понять где идет наибольшее накопление погрешностей и исправить ошибку.

Вариант задания