|
…
|
||
|---|---|---|
| .. | ||
| ConsoleApp1 | ||
| pic | ||
| .gitignore | ||
| README.md | ||
Отчет по лабораторной работе №6
Выполнил студент гр. ИСЭбд-41 Миронов Е.О.
Выбор алгоритма
Предложенный алгоритм(теорема Лапласа) имеет асимптотику примерно O(n!). Для подсчета определителя матрицы размерностью более 10х10 он зависает. Запустить его на матрицу 100х100 на моей машине просто невозвожно.
Поэтому рассматриваю другой алгоритм - метод Гаусса. Он имеет сложность O(n^3), и его уже реально выполнять на больших данных. Но на каждом шаге изменяется общий ресурс в виде исходной матрицы, поэтому алгоритм должен плохо параллелиться.
Также ко всему этому определитель матрицы свыше 100х100 слишком большой и не поддерживается типом double.
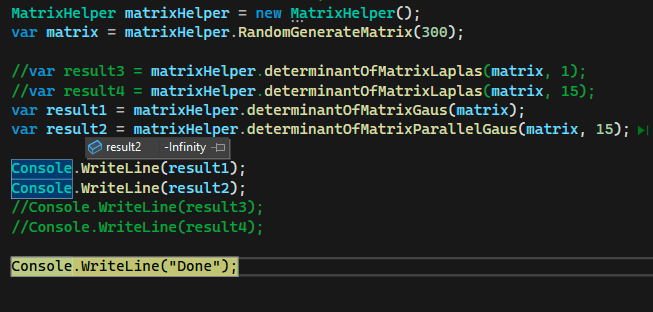
В итоге решил использовать теорему Лапласа на матрицах до 10х10 и метод Гаусса на матрицах до 100х100
Создание приложения
Выбрал язык C#, Консольное приложение.
Попробуем запустить все алгоритмы на матрицах 3х3 и проверить результат выполнения.
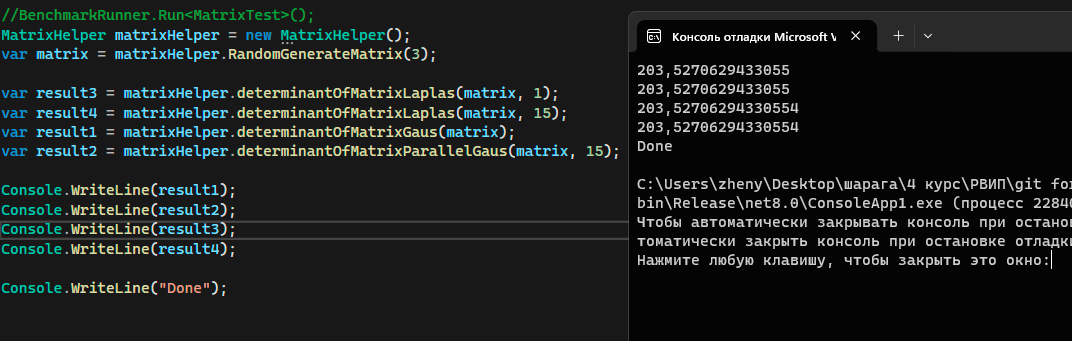
Немного разные результаты спишу на погрешность типа double
Однопоточный метод Гаусса
public double determinantOfMatrixGaus(double[,] mat, int n)
{
int i, j, k;
for (i = 0; i < n - 1; i++)
{
for (j = i + 1; j < n; j++)
{
if (j == i)
continue;
double someDet = mat[j, i] / mat[i, i];
for (k = i; k < n; k++)
mat[j, k] -= someDet * mat[i, k];
}
}
double det = 1;
for (i = 0; i < n; i++)
det = det * mat[i, i];
return det;
}
Параллельный метод Гаусса
public double determinantOfMatrixParallelGaus(double[,] mat, int n)
{
Parallel.For(0, n - 1,
new ParallelOptions()
{
MaxDegreeOfParallelism = threadCount
},
(i) =>
{
for (int j = i + 1; j < n; j++)
{
if (j == i)
continue;
double det = mat[j, i] / mat[i, i];
for (int k = i; k < n; k++)
mat[j, k] = mat[j, k] - det * mat[i, k];
};
});
double det = 1;
for (int i = 0; i < n; i++)
det = det * mat[i, i];
return det;
}
Почему это работает до конца не понятно. Возможно потому что алгоритм меняет только строку j, и только на основании данных строк i (счетчик в Parallel.For - синхронизован) и j(текущая строка).
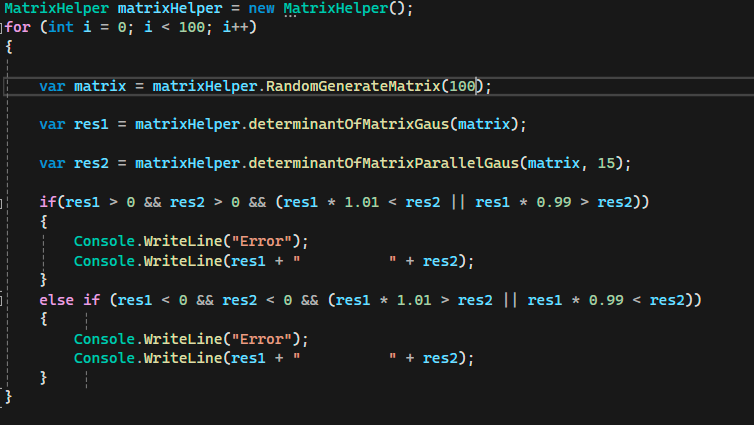
Сделал вот такую проверку - все ок, ни одной ошибки
Однако я все равно сомневаюсь в прошлой реализации и подозреваю, что где-то есть race condition. Поэтому вот реализация в которой куча блокировок, и она работает намного медленее, но зато я в ней уверен.
public double determinantOfMatrixParallelGaus(double[,] mat, int n)
{
lockObjects = new object[n].Select(x => new object()).ToArray();
for (int i = 0; i < n - 1; i++)
{
lock (lockObjects[i])
{
Parallel.For(i + 1, n,
(j) =>
{
if (j == i)
return;
lock (lockObjects[j])
{
double det = mat[j, i] / mat[i, i];
for (int k = i; k < n; k++)
mat[j, k] = mat[j, k] - det * mat[i, k];
}
});
}
}
double det = 1;
for (int i = 0; i < n; i++)
det = det * mat[i, i];
return det;
}
Бенчмарки
Запускаю тесты
- Лаплас 10х10 в один поток
- Лаплас 10х10 в 15 потоков
- Гаусс 10х10 в 15 потоков
- Гаусс 10х10 в 1 поток
- Гаусс 100х100 в 15 потоков
- Гаусс 100х100 в 1 поток.
Видим, что в нашем тесте параллельные реализации работают быстрее однопоточных.
Помимо этого и без того понятного вывода видим огромную разницу в алгоритмах Гаусса и Лапласа. С объемом данных большим в 100 раз алгоритм Гаусса справляется быстрее в 40 раз. При этом он является оптимальным по памяти и практически не создает нагрузки на сборщик мусора.