IIS_2023_1/zhukova_alina_lab_5

Задание

Использовать метод регрессии по варианту для выбранных данных, самостоятельно сформулировав задачу. Интерпретировать результаты и оценить, насколько хорошо он подходит для решения сформулированной вами задачи

Вариант №10

Используемые технологии

В лабораторной были использованы библиотеки:

• pandas - позволяет работать с наборами данных
• matplotlib - используется для создания графиков
• sklearn - используется для работы с моделями и методами машинного обучения
• numpy - позволяет работать с массивами и матрицами
• Flask - предоставляет способ быстрого создания веб-страниц для визуализации работы приложения

Используемые компоненты

• LinearRegression - библиотечная реализация метода линейной регрессии, алгоритм стремится с помощью зависимости целевой переменной от одного или нескольких параметров построить линию, наиболее точно описывающую массив данных
• accuracy_score - метрика измерения точности для определения качества регресии
• mean_absolute_error - метрика измерения точности регресии через среднюю абсолютную ошибку

Как запустить

Запустить файл flask-server, который поднимет локальный сервер и позволит обратиться к программе через браузер по ссылке http://127.0.0.1:5000/

Что делает программа

Берет 5000 записей из датасета (датасет Chess Game Dataset) https://www.kaggle.com/datasets/datasnaek/chess), Преобразует данные нечисловых столбцов в числовые значения, осуществляет нормализацию и взвешивание параметров. Строит регрессионную зависимость используя модель LinearRegression, Оценивает качество полученной модели с помощью метрик accuracy_score и mean_absolute_error

Анализ и скриншоты работы программы

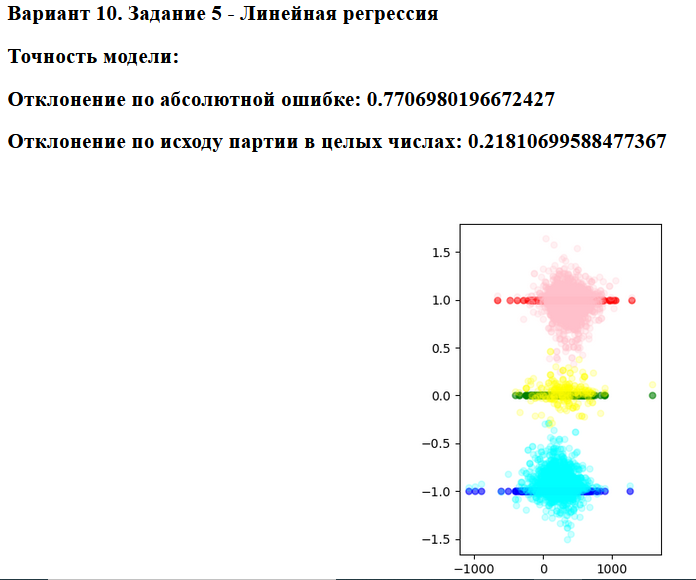
С помощью регрессии планировалось получить предсказание об исходе партий, а именно вероятность победы того или иного игрока. Предсказание строиться исходя из ходов в шахматной записи, каждому из которого присваивается своя ценность, а также учитывается рейтинг игроков и открывающая комбинация ходов.

Судить о модели можно и по средней абсолютной ошибке, но намного проще воспринимать ее по точности данных предсказаний. Отклонение по исходу партии представляет точность модели как процент неверных ответов об исходе партии. Так как регрессионная модель выдает результаты от -1 до +1, а нам нужно получить исход игры, значения из регресии с помощью специальной фунции приводятся к одному числу из -1, 0, +1, где 0 означает ничью, +1 победу игрока играющего белыми, -1 победу игрока играющего черными. Таким образом, модель даст верный ответ в 79% случаев