Лабораторная работа 6
Вариант 10
Задание:
- Используя данные из "F1DriversDataset.csv" сформулировать задачу, решаемую нейронной сетью (MLPRegressor): Предсказать количество чемпионских титулов по характеристикам:
Race_Entries,Race_Starts,Pole_Positions,Race_Wins,Podiums,Fastest_Laps
Запуск
- Запустить файл lab6.py
Технологии
- Язык - 'Python'
- Библиотеки sklearn, pandas, matplotlib
Что делает
- Программа обучает нейронную модель на 95% данных (Были подобраны следующие настройки модели - 20 слоев и 20 нейронов в каждом, большие или меньшие значения приводили к переобучению или недообучению, solver - для оптимизации был выбран алгоритм adam на основе стохастического градиента, activation - функция активации скрытых слоев был выбран relu выпрямленная линейная единица измерения)
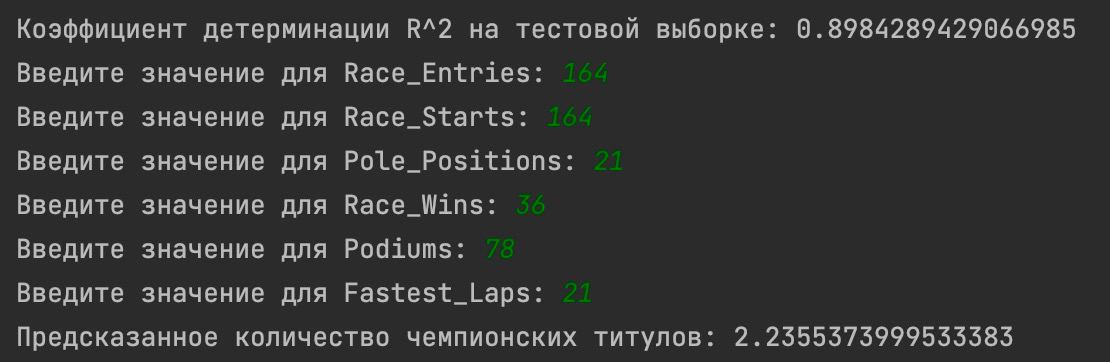
- Программа оценивает качество предсказаний, используя Коэффициент детерминации R^2 (Мера качества модели регрессии и оценивает, насколько хорошо модель соответствует данным. Она измеряет долю дисперсии зависимой переменной, которая может быть объяснена моделью, относительно общей дисперсии зависимой переменной) на тестовой выборке остальных 5%
- Программа позволяет вручную ввести требуемые характеристики пилота и предсказать количество титулов для данного пилота
- Также результат предсказания можно интерпретировать в другом ключе: если мы введем реальные характеристики гонщика, мы можем посмотреть, насколько он достоин быть титулованным, справедливо или несправедливо отнеслась к нему судьба:)
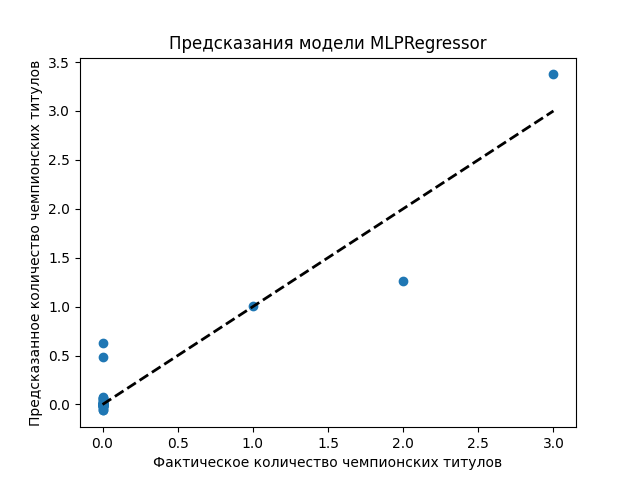
- Программа дополнительно выводит график, позволяющий визуально определить качество работы модели
Пример работы
Пример работы представлен в виде скриншотов:
- В результате по графику мы можем видеть, что нейронная модель неплохо справилась со своей задачей предсказания, это подтверждает и хороший R^2 коэффициент, равный 0.8984, что на несколько тысячных лучше, чем Линейная регрессия на тех же данных.
- В качестве реального гонщика был выбран действующий чемпион Формулы 1 - Макс Ферстаппен. В отличие от линейной регрессии, модель правильно предсказала два чемпионских титула (в сокращении), при этом показатель 2.23 говорит о потенциале на 3 титул (что оправдается в 23 году)