Alexey/IIS_2023_1

History

DmitriyAntonov 8a288f0abf iter3		2023-09-23 20:53:45 +04:00
..
screens	iter3	2023-09-23 20:53:45 +04:00
lab1.py	iter3	2023-09-23 20:53:45 +04:00
README.md	iter3	2023-09-23 20:53:45 +04:00

README.md

Лаб 1

Работа с типовыми наборами данных и различными моделями

Вариант 3

Данные: make_classification (n_samples=500, n_features=2, n_redundant=0, n_informative=2, random_state=rs, n_clusters_per_class=1)

Модели:

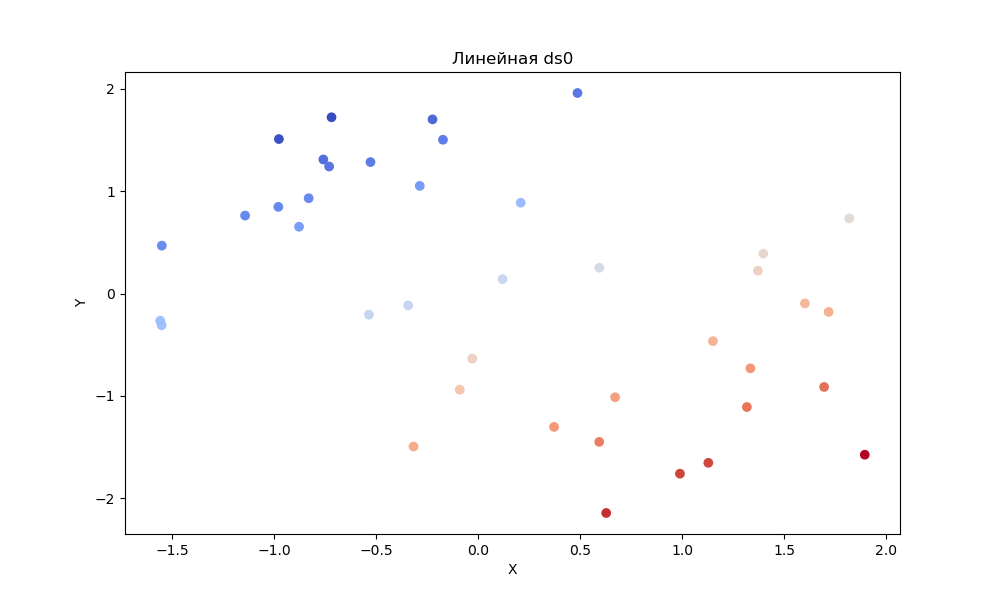
Линейную регрессию
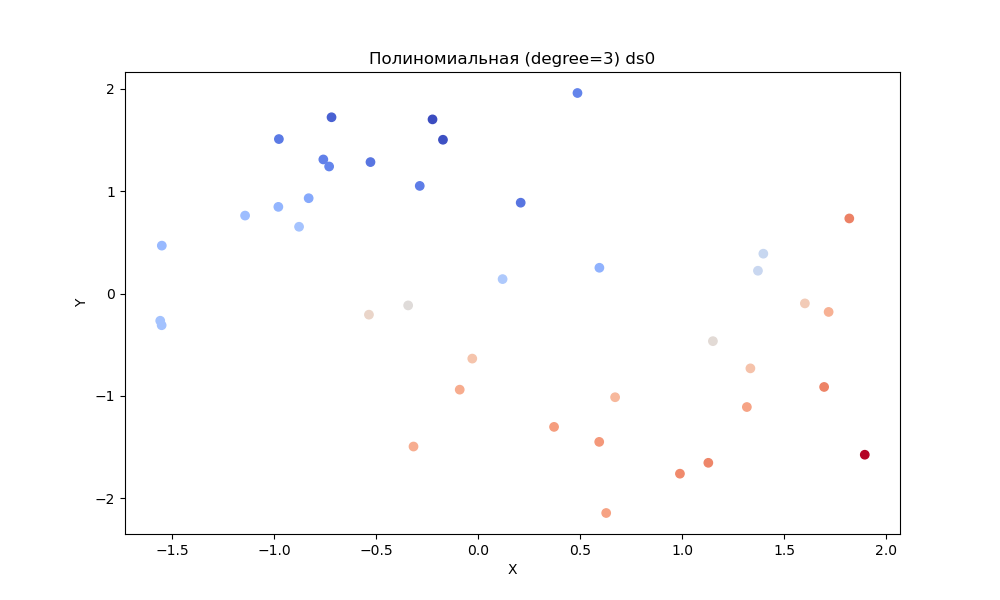
Полиномиальную регрессию (со степенью 3)
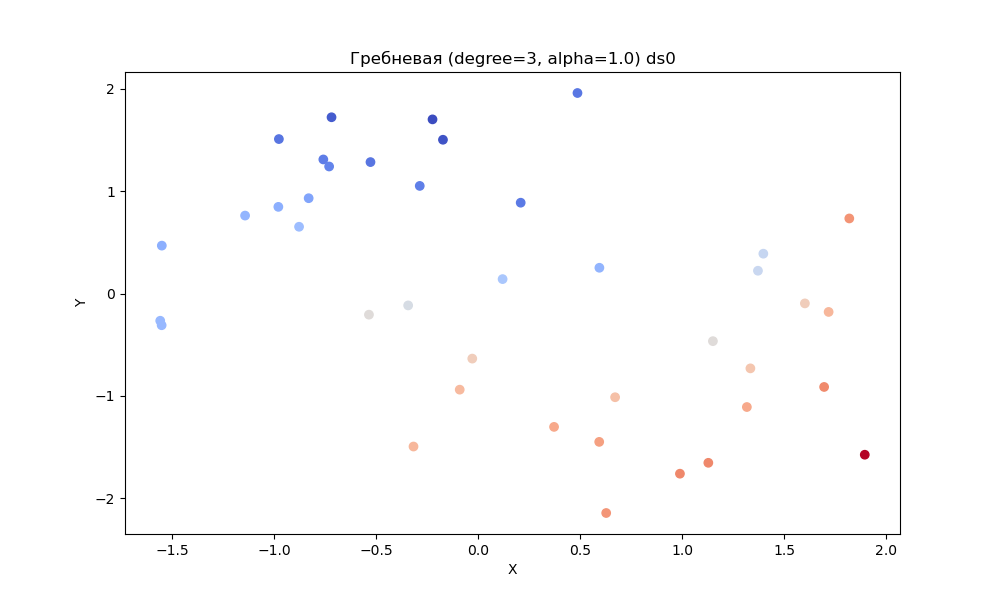
Гребневую полиномиальную регрессию (со степенью 3, alpha = 1.0)

Графики

Качество каждой модели может быть оценено на основе среднеквадратичной ошибки (MSE). Более низкий MSE указывает на лучшее соответствие данным. Однако выбор модели зависит от набора данных и лежащей в основе взаимосвязи между объектами и целевой переменной.

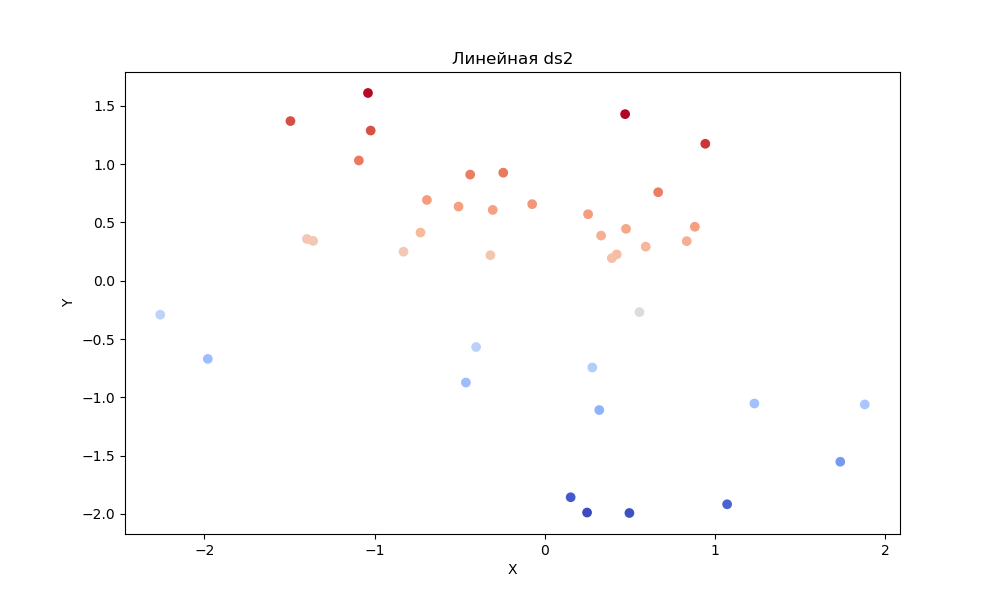
Линейная регрессия: Линейная регрессия предполагает линейную зависимость между признаками и целевой переменной. Это хорошо работает, когда взаимосвязь линейна, а шум в наборе данных минимален. Лучше всего сработала на наборе лун. Хуже всего на кругах. На линейном наборе показала себя на равне с остальными.

Полиномиальная и гребневая показали примерно одинаково на всех наборах.

Полиномиальная регрессия (степень=3): Полиномиальная регрессия обеспечивает более гибкую подгонку за счет полинома более высокого порядка(кубическая кривая). Она может выявить более сложные взаимосвязи между объектами и целевой переменной. Она может сработать лучше, чем линейная регрессия, если истинная взаимосвязь нелинейна.

Гребневая регрессия (степень= 3, альфа=1,0): В случае полиномиальной регрессии с регуляризацией (альфа=1,0) модель добавляет коэффициент регуляризации для управления сложностью обучения. Регуляризация помогает предотвратить переобучение, когда набор данных содержит шум или когда он ограничен.

Набор лун (moon_dataset)