Лабораторная работа 1. Вариант 15
Задание
Сгенерировать данные:
make_classification (n_samples=500, n_features=2, n_redundant=0, n_informative=2, random_state=rs, n_clusters_per_class=1)
Сравнить на нем 3 модели:
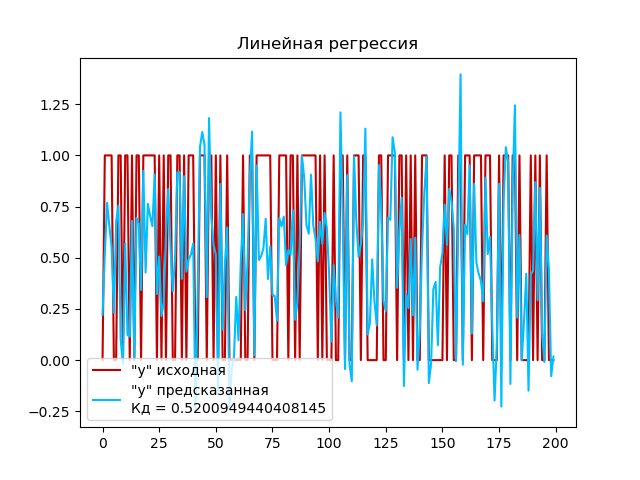
- Линейную регрессию
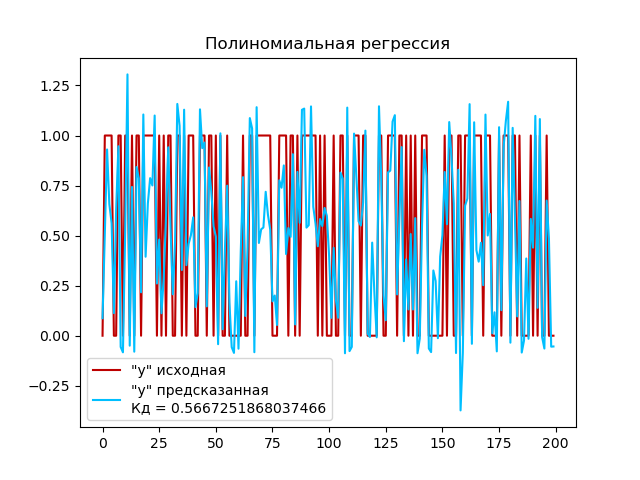
- Полиномиальную регрессию (со степенью 4)
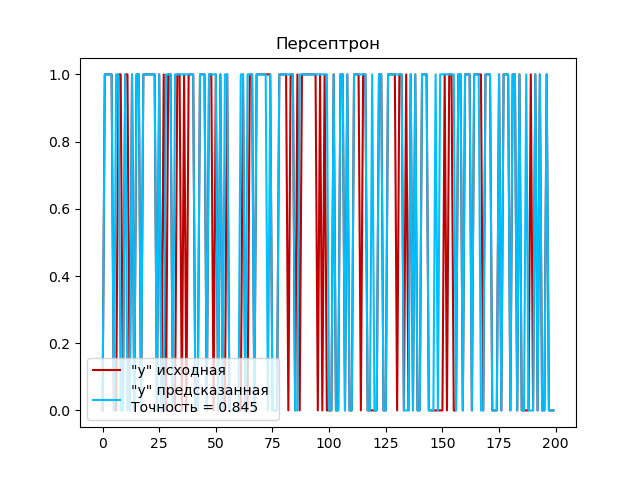
- Персептрон
Как запустить лабораторную работу
Для запуска программы необходимо с помощью командной строки в корневой директории файлов прокета прописать:
python main.py
Какие технологии использовали
- Библиотека numpy для работы с массивами.
- Библиотека matplotlib pyplot - для визуализации данных.
- Библиотека sklearn:
- make_classification для создания синтетических наборов данных.
- LinearRegression для создания и работы с моделью Линейной регрессии.
- Perceptron для создания и работы с Персептроном
- accuracy_score для использования функции, используемая для вычисления точности классификации.
- train_test_split для разделения набора данных на обучающую и тестовую выборки.
- PolynomialFeatures для создания преобразователя, который генерирует полиномиальные признаки из исходных признаков
Описание лабораторной работы
Генерация данных
Программа создает синтетический набор данных, где переменная X будет содержать матрицу признаков размером (n_samples, n_features), а переменная y будет содержать вектор целевых переменных размером (n_samples,).
X, y = make_classification(n_samples=500, n_features=2, n_redundant=0,
n_informative=2, random_state=None,
n_clusters_per_class=1)
Добавляет шум к данным путем увеличения значений матрицы признаков X на случайные значения из равномерного распределения, умноженные на 2. Затем создает переменную, которая содержит кортеж из матрицы признаков X и вектора целевых переменных y. И разделяет данные на обучающий набор (X_train, y_train) и тестовый набор (X_test, y_test) с помощью функции train_test_split. Обучающий набор составляет 60% от исходных данных, а 40% от исходных данных используются для тестирования модели (test_size=.4).
rng = np.random.RandomState(2)
X += 2 * rng.uniform(size=X.shape)
linearly_dataset = (X, y)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4, random_state=42)
Работа с моделью линейной регрессии
Создаем экземпляр модели линейной регрессии с помощью класса LinearRegression(), которая будет использоваться для построения линейной регрессии. Обучаем модель на обучающем наборе данных X_train и y_train с помощью метода fit(). Затем используем обученную модель для прогнозирования целевых переменных на тестовом наборе данных X_test с помощью метода predict(). Полученные прогнозы сохраняются в переменную y_pred. И вычисляем коэффициент детерминации (R-квадрат) для для оценки качества модели регрессии на тестовом наборе данных с помощью метода score().
# Модель линейной регрессии
model = LinearRegression()
# Обучение на тренировочных данных
model.fit(X_train, y_train)
# Выполнение прогноза
y_pred = model.predict(X_test)
# Вычисление коэффициента детерминации
r_sq = model.score(X_test, y_test)
Выполним построение графика:
Работа с моделью полиномиальной регрессии (со степенью 4)
Создаем экземпляр класса PolynomialFeatures для генерации полиномиальных признаков со степень полинома 4 и параметр include_bias=False, чтобы исключить добавление дополнительного столбца с единицами (смещения). Преобразуем обучающий набор данных X_train и тестовый набор данных X_test в полиномиальные признаки с помощью метода fit_transform() и сохраняем в переменные X_poly_train и X_poly_test соотвественно. Создаем экземпляр модели линейной регрессии с помощью класса LinearRegression(). Обучаем модель линейной регрессии на обучающем наборе данных X_poly_train и y_train с помощью метода fit(). Используем обученную модель для прогнозирования целевых переменных на тестовом наборе данных X_poly_test с помощью метода predict(). И вычисляем коэффициент детерминации (R-квадрат) для модели на тестовом наборе данных с помощью метода score().
pf = PolynomialFeatures(degree=4, include_bias=False)
# Преобразование исходного набора данных X_train в полиномиальные признаки
X_poly_train = pf.fit_transform(X_train)
# Преобразование исходного набора данных X_test в полиномиальные признаки
X_poly_test = pf.fit_transform(X_test)
# Модель линейной регрессии
model = LinearRegression()
# Обучение модели линейной регрессии на преобразованных полиномиальных признаках
model.fit(X_poly_train, y_train)
# Выполнение прогноза
y_pred = model.predict(X_poly_test)
# Вычисление коэффициента детерминации
r_sq = model.score(X_poly_test, y_test)
Выполним построение графика:
Работа с персептроном
Создаем экземпляр модели персептрона model = Perceptron() и обучаем модель на тренировочных данных с помощью метода fit(). После обучения модели персептрона, выполняем прогноз на тестовых данных с помощью метода predict(). Для оценки точности работы персептрона используем функцию accuracy_score, которая сравнивает предсказанные классы y_pred с истинными классами y_test и возвращает долю правильно классифицированных примеров.
# Модель персептрона
model = Perceptron()
# Обучение на тренировочных данных
model.fit(X_train, y_train)
# Выполнение прогноза
y_pred = model.predict(X_test)
# Вычисление точности работы персептрона
accuracy = accuracy_score(y_test, y_pred)
Выполним построение графика:
Вывод
Исходя из построенных графиков можно сделать следующий вывод:
-
Коэффициент детерминации для полиномиальной регрессии (0,56) выше, чем для линейной регрессии (0,52). Это означает, что полиномиальная модель лучше объясняет изменчивость в данных, чем линейная модель. Однако значение 0.56 указывает на некоторую связь между предсказываемой переменной и независимыми переменными, но остается возможность для дальнейшего улучшения модели.
-
Доля правильно классифицированных примеров персептроном (0,845) также высокая. Это говорит о том, что персептрон успешно выполнил задачу классификации и хорошо разделил примеры на правильные классы.
В целом, можно сделать вывод, что и полиномиальная регрессия и персептрон проявляют лучшую производительность и демонстрируют лучшие результаты в анализе сгенерированных нами данных, чем линейная регрессия.