Лабораторная работа 6.
Задание
Задачи:
Реализовать нахождение детерминанта квадратной матрицы. Сделать два алгоритма: обычный и параллельный (задание со * - реализовать это в рамках одного алгоритма). В параллельном алгоритме предусмотреть ручное задание количества потоков (число потоков = 1 как раз и реализует задание со *), каждый из которых будет выполнять нахождение отдельной группы множителей.
Как запустить лабораторную работу
В директории с файлом характеристик docker-compose.yaml выполнить команду:
docker-compose -f docker-compose.yaml up
Описание лабораторной работы
Для реализации параллельного нахождения детерминанта квадратной матрицы с использованием многопоточности создадим несколько функций:
- Функция
calculate_determinant(args)
Данная функция принимает матрицу и номер элемента, по которому ищется минор. Если i нечетное число, множитель умножается на -1.
Удаляет первую строку из matrix с помощью функции np.delete(matrix, 0, axis=0).
Удаляет столбец i из matrix с помощью функции np.delete(matrix, i, axis=1).
Возвращает определитель полученной подматрицы, умноженный на множитель.
def calculate_determinant(args):
matrix, i = args
multiplier = matrix[0][i]
if i % 2 != 0:
multiplier *= -1
matrix = np.delete(matrix, 0, axis=0)
submatrix = np.delete(matrix, i, axis=1)
return np.linalg.det(submatrix) * multiplier
- Функция
parallel_determinant(matrix, parallel)
Данная функция принимает матрицу, для которой нужно вычислить определитель, и флаг, указывающий, следует ли использовать параллельное вычисление. Далее вычисляется размер матрицы n с помощью matrix.shape[0]. Если флаг указывает на использование параллельного вычисления, создается пул процессов с n процессами с помощью Pool(processes=n). Затем создается цикл по значениям от 0 до n.
Для каждого значения i добавляет в список results результат выполнения функции calculate_determinant с аргументами matrix и i. Затем закрывается пул процессов и ожидается завершения всех процессов с помощью pool.close() и pool.join(). Далее суммируются все значения из списка results с помощью np.sum([res.get() for res in results]), сохраняет результат в переменную result и также вычисляется затраченное время на вычисление определителя.
- Функция
test(parallel)
Данная функция принимает значение флага, указывающего на использование параллельного или обычного вычисления. Также создает матрицу mx размером 3x3 и выполняет вычисление определителя матрицы mx с помощью функции parallel_determinant(mx, parallel).
- Функции
matrix10x10(parallel),matrix25x25(parallel)иmatrix50x50(parallel)
Т.к. на моем устройстве не возможно вычислять детерминат матрицы размером более 100х100, то вместо использования матриц размером 100x100, 300x300, 500x500 элементов были созданы матрицы 10х10, 25х25, 50х50.
В функциях matrix10x10(parallel), matrix25x25(parallel) и matrix50x50(parallel) принимается аргумент parallel, указывающий, следует ли использовать параллельное вычисление. Создаются матрицы размером 10x10, 25x25 и 50x50 со случайными целочисленными значениями от 0 до 100. И выполяются вычисления определителя для каждой матрицы с помощью функции parallel_determinant.
Результаты выполнения последовательного и параллельного алгоритма на вычисление детерминанта квадратных матриц 10х10, 25х25, 50х50.
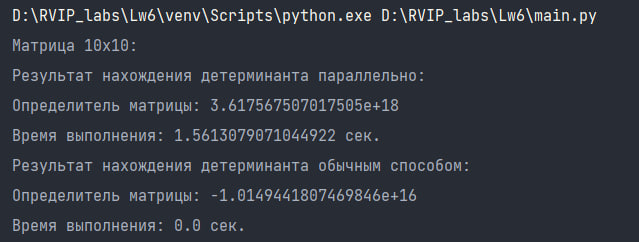
Результат вычисления детерминанта матрицы 10х10:
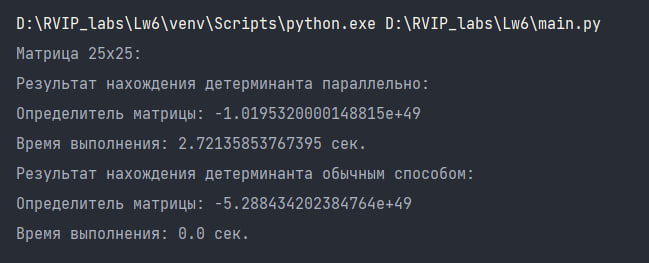
Результат вычисления детерминанта матрицы 25х25:
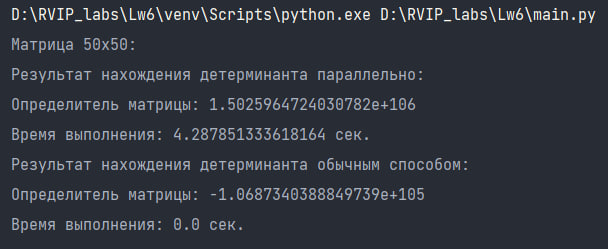
Результат вычисления детерминанта матрицы 50х50:
Таким образом, можно сделать вывод о том, что вычисления обычным алгоритмом выполняются быстрее, чем при использовании параллельного способа нахождения детерминанта. Если точность результата является наиболее приоритетным фактором, то использование параллельного способа может быть предпочтительным. В случае, когда время выполнения играет решающую роль, обычный алгоритм может быть более эффективным выбором. Кроме того, для дальнейшего улучшения производительности вычислений можно рассмотреть возможность оптимизации параллельного способа нахождения детерминанта, например, с использованием более эффективных алгоритмов или распределения вычислений на более мощные вычислительные узлы.