| .. | ||
| screenshots | ||
| src | ||
| .gitignore | ||
| lab5.mp4 | ||
| README.md | ||
Лабораторная работа №5
Задание
Кратко: реализовать умножение двух больших квадратных матриц.
Подробно: в лабораторной работе требуется сделать два алгоритма: обычный и параллельный. В параллельном алгоритме предусмотреть ручное задание количества потоков, каждый из которых будет выполнять умножение элементов матрицы в рамках своей зоны ответственности.
Ход работы
Последовательный алгоритм
public static int[][] multiplyMatricesSequential(int[][] matrix1, int[][] matrix2) {
int rows1 = matrix1.length;
int columns1 = matrix1[0].length;
int columns2 = matrix2[0].length;
int[][] result = new int[rows1][columns2];
for (int i = 0; i < rows1; i++) {
for (int j = 0; j < columns2; j++) {
for (int k = 0; k < columns1; k++) {
result[i][j] += matrix1[i][k] * matrix2[k][j];
}
}
}
return result;
}
Параллельный алгоритм
public static int[][] multiplyMatricesParallel(int[][] matrix1, int[][] matrix2) {
int rows1 = matrix1.length;
int columns1 = matrix1[0].length;
int columns2 = matrix2[0].length;
int[][] result = new int[rows1][columns2];
int numberOfThreads = 5; // Количество потоков
ExecutorService executor = Executors.newFixedThreadPool(numberOfThreads);
for (int i = 0; i < rows1; i++) {
final int row = i;
executor.execute(new Runnable() {
@Override
public void run() {
for (int j = 0; j < columns2; j++) {
for (int k = 0; k < columns1; k++) {
result[row][j] += matrix1[row][k] * matrix2[k][j];
}
}
}
});
}
executor.shutdown();
while (!executor.isTerminated()) {
// Ожидаем завершения всех потоков
}
return result;
}
Результат
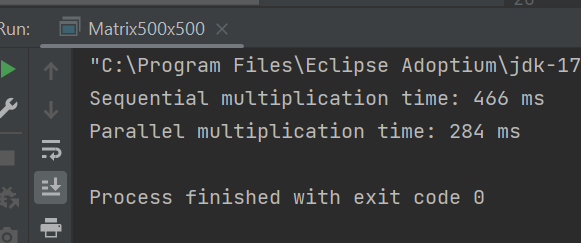
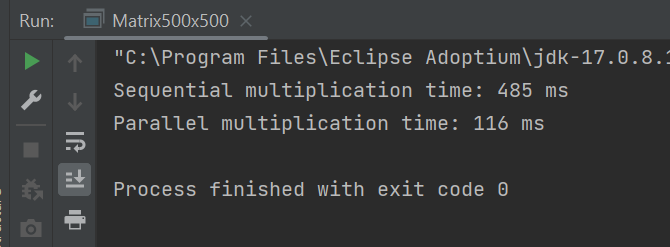
Была проверка времени выполнения алгоритма для матриц размером 100х100, 300х300, 500х500 с разным количеством потоков.
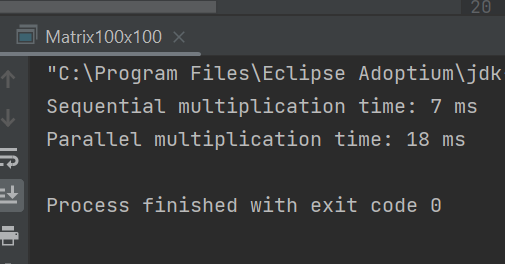
100х100, 1 поток
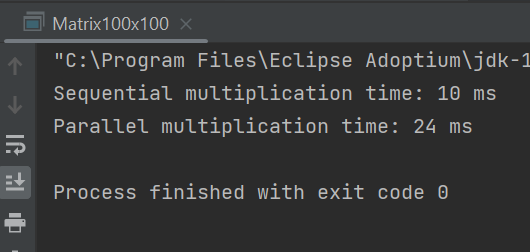
100х100, 5 потоков
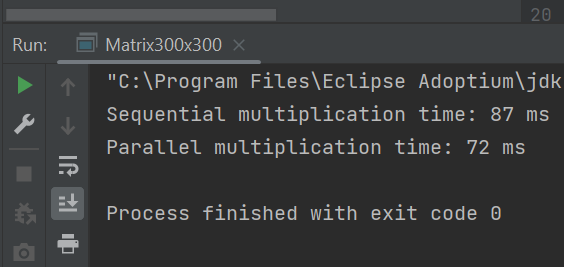
300х300, 1 поток
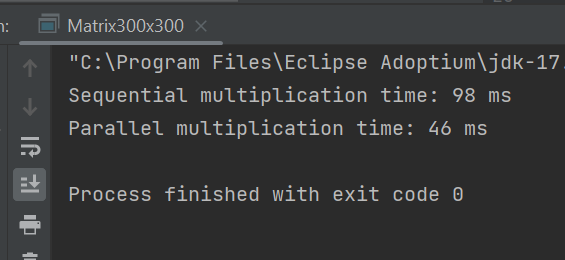
300х300, 5 потоков
500х500, 1 поток
500х500, 5 потоков
Из данных скриншотов видно, что в случае с матрицей 100х100 последовательный алгоритм работает лучше, чем параллельный.
Для остальных матриц параллельный алгоритм работает лучше, а также увеличение кол-ва потоков уменьшает время выполнения алгоритма. (хотя в случае матрицы 100х100 - сильно увеличивает)
Работоспособность показана в видео: lab5.mp4