| .. | ||
| src | ||
| .gitignore | ||
| img.png | ||
| lab6.mp4 | ||
| README.md | ||
Лабораторная работа №6
Задание
Кратко: реализовать нахождение детерминанта квадратной матрицы.
Подробно: в лабораторной работе требуется сделать два алгоритма: обычный и параллельный. В параллельном алгоритме предусмотреть ручное задание количества потоков, каждый из которых будет выполнять нахождение отдельной группы множителей.
Ход работы
Обычный алгоритм
private static BigDecimal findDeterminantGauss(double[][] matrix) {
int n = matrix.length;
BigDecimal det = BigDecimal.ONE;
for (int i = 0; i < n; i++) {
int maxRow = i;
for (int j = i + 1; j < n; j++) {
if (Math.abs(matrix[j][i]) > Math.abs(matrix[maxRow][i])) {
maxRow = j;
}
}
if (maxRow != i) {
double[] temp = matrix[i];
matrix[i] = matrix[maxRow];
matrix[maxRow] = temp;
det = det.multiply(BigDecimal.valueOf(-1));
}
for (int j = i + 1; j < n; j++) {
double factor = matrix[j][i] / matrix[i][i];
for (int k = i; k < n; k++) {
matrix[j][k] -= factor * matrix[i][k];
}
}
}
for (int i = 0; i < n; i++) {
det = det.multiply(BigDecimal.valueOf(matrix[i][i]));
}
return det;
}
Параллельный алгоритм
private static BigDecimal findDeterminantGaussParallel(double[][] matrix, int threadsCount) {
int n = matrix.length;
final BigDecimal[] det = {BigDecimal.ONE};
ExecutorService executor = Executors.newFixedThreadPool(threadsCount);
for (int i = 0; i < n; i++) {
final int rowIdx = i;
int maxRow = rowIdx;
for (int j = rowIdx + 1; j < n; j++) {
if (Math.abs(matrix[j][rowIdx]) > Math.abs(matrix[maxRow][rowIdx])) {
maxRow = j;
}
}
if (maxRow != rowIdx) {
double[] temp = matrix[rowIdx];
matrix[rowIdx] = matrix[maxRow];
matrix[maxRow] = temp;
det[0] = det[0].multiply(BigDecimal.valueOf(-1));
}
executor.execute(() -> {
for (int j = rowIdx + 1; j < n; j++) {
double factor = matrix[j][rowIdx] / matrix[rowIdx][rowIdx];
for (int k = rowIdx; k < n; k++) {
matrix[j][k] -= factor * matrix[rowIdx][k];
}
}
});
det[0] = det[0].multiply(BigDecimal.valueOf(matrix[rowIdx][rowIdx]));
}
executor.shutdown();
try {
executor.awaitTermination(1, TimeUnit.DAYS);
} catch (InterruptedException e) {
e.printStackTrace();
}
return det[0];
}
Результат
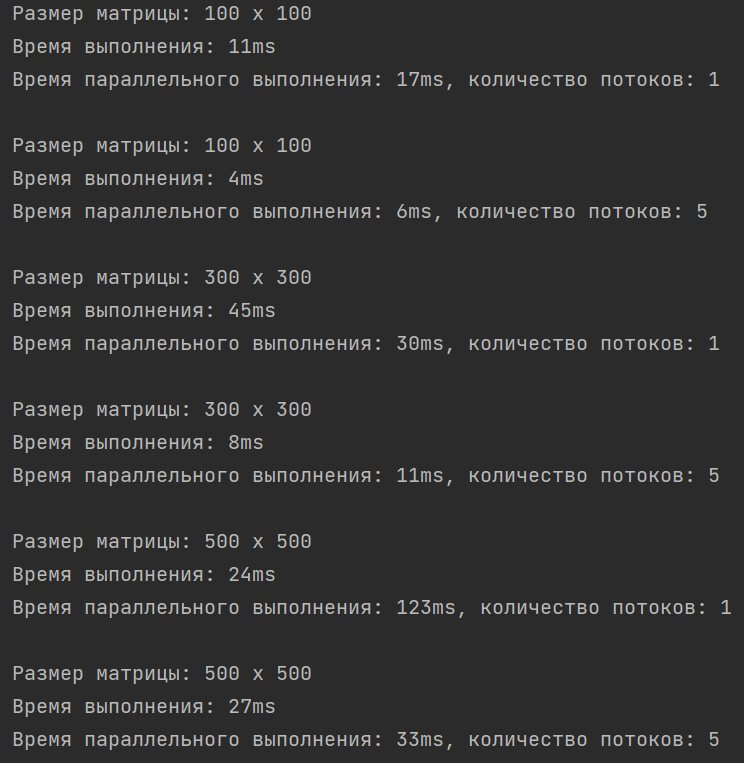
Была проверка времени выполнения алгоритма для матриц размером 100х100, 300х300, 500х500 с разным количеством потоков.
Из данного скриншота можно сделать вывод, что нахождение детерминанта для матрицы:
- 100х100 - обычный алгоритм работает лучше параллельного, но разница не сказать что значительная
- 300х300 - обычный алгоритм работает хуже параллельного, но при добавлении потоков параллельный алгоритм работает чуть хуже
- 500х500 - обычный алгоритм работает значительно лучше параллельного, но параллельный начинает показывать себя лучше при увеличении количества потоков (но обычный алгоритм все равно лучше)
Работоспособность показана в видео: lab6.mp4